题目内容
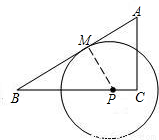
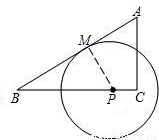
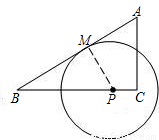
(2009•永嘉县二模)如图,Rt△ABC的两条直角边AC=3,BC=4,点P是边BC上的一动点(P不与B重合),以P为圆心作⊙P与BA相切于点M.设CP=x,⊙P的半径为y.(1)求证:△BPM∽△BAC;
(2)求y与x的函数关系式,并确定当x在什么范围内取值时,⊙P与AC所在直线相离;
(3)当点P从点C向点B移动时,是否存在这样的⊙P,使得它与△ABC的外接圆相内切?若存在,求出x、y的值;若不存在,请说明理由.
【答案】分析:(1)由∠B=∠B,∠C=∠BMP=90°证明;
(2)勾股定理求出AB的长,相似三角形求出y与x的函数关系式,求出取值范围;
(3)根据内切圆的特点,求出x,y的值.
解答: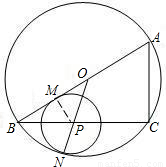 (1)证明:∵AB切⊙P于点M,
(1)证明:∵AB切⊙P于点M,
∴∠PMB=∠C=90°.
又∵∠B=∠B,
∴△BPM∽△BAC.
(2)解:∵AC=3,BC=4,∠C=90°,
∴AB=5.
∵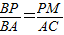 ,
,
∴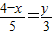 ,
,
∴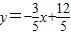 (0≤x<4).
(0≤x<4).
当x>y时,⊙P与AC所在的直线相离.
即x>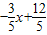 ,
,
得x> ,
,
∴当 <x<4时,⊙P与AC所在的直线相离.
<x<4时,⊙P与AC所在的直线相离.
(3)解:设存在符合条件的⊙P.
得OP=2.5-y,而BM=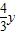 ,
,
∴OM=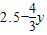 ,
,
有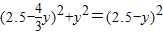 ,
,
得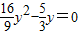
∴y1=0(不合题意舍去),y2= .
.
∴ 时,x=
时,x=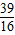 .
.
点评:本题涉及的知识点较多,综合考查了相似三角形的应用和待定系数法求一次函数解析式.
(2)勾股定理求出AB的长,相似三角形求出y与x的函数关系式,求出取值范围;
(3)根据内切圆的特点,求出x,y的值.
解答:
 (1)证明:∵AB切⊙P于点M,
(1)证明:∵AB切⊙P于点M,∴∠PMB=∠C=90°.
又∵∠B=∠B,
∴△BPM∽△BAC.
(2)解:∵AC=3,BC=4,∠C=90°,
∴AB=5.
∵
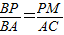 ,
,∴
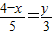 ,
,∴
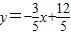 (0≤x<4).
(0≤x<4).当x>y时,⊙P与AC所在的直线相离.
即x>
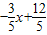 ,
,得x>
 ,
,∴当
 <x<4时,⊙P与AC所在的直线相离.
<x<4时,⊙P与AC所在的直线相离.(3)解:设存在符合条件的⊙P.
得OP=2.5-y,而BM=
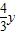 ,
,∴OM=
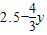 ,
,有
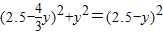 ,
,得
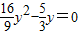
∴y1=0(不合题意舍去),y2=
 .
.∴
 时,x=
时,x=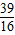 .
.点评:本题涉及的知识点较多,综合考查了相似三角形的应用和待定系数法求一次函数解析式.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
(2009•永嘉县二模)我国上海将于2010年举办世博会,今年温州某小商品企业获得了“上海世博会”生产纪念徽章的许可证.为了满足市场需求,该企业现在开始生产A,B两种款式的纪念徽章,每天共生产4500个;两种纪念徽章的成本和售价如下表所示,设每天生产A种的纪念徽章x个,每天共获利y元.
(1)求出y与x之间的函数关系;
(2)如果该企业每天投入成本不超过10000元,那么每天最多获利多少元?
| 款式 | 成本(元/个) | 售价(元/个) |
| A | 2 | 2.3 |
| B | 3 | 3.5 |
(2)如果该企业每天投入成本不超过10000元,那么每天最多获利多少元?