题目内容
4.已知一次函数y=$\frac{1-kx}{k+1}$(k是不为0的自然数,且是常数)的图象与两坐标轴所围成的图形的面积为Sk(即k=1时,得S1,k=2时,得S2,┅).试求S1+S2+S3+…+S2016=$\frac{1008}{2017}$.分析 令x=0,y=0,分别求出图象与坐标轴的交点,再根据三角形面积公式表示S1,S2,S3,…S2016,根据规律求和.
解答 解:令x=0,得y=$\frac{1}{k+1}$,y=0,得x=$\frac{1}{k}$,
∴S=$\frac{1}{2}$×$\frac{1}{k+1}$×$\frac{1}{k}$=$\frac{1}{2}$($\frac{1}{k}$-$\frac{1}{k+1}$),
∴S1+S2+S3+…+S2016,
=$\frac{1}{2}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$),
=$\frac{1}{2}$(1-$\frac{1}{2017}$),
=$\frac{1008}{2017}$.
故答案为:$\frac{1008}{2017}$.
点评 本题考查了一次函数图象上的点的坐标特征.关键是由函数关系式求直线与坐标轴的交点坐标,得出三角形面积的一般关系式,寻找抵消规律.

练习册系列答案
相关题目
14.在下列各组数中,是勾股数的一组是( )
| A. | 0.3、0.4、0.5 | B. | $\frac{3}{5}$、$\frac{4}{5}$、1 | C. | 25、7、24 | D. | 6、5、4 |
15.下列方程是一元一次方程的是( )
| A. | 4x+2y=3 | B. | y+5=0 | C. | x2=2x-l | D. | $\frac{1}{y}$+y=2 |
12.解方程$\frac{3x+1}{2}$-$\frac{10x+1}{6}$=2时,去分母、去括号后,正确结果是( )
| A. | 9x+1-10x+1=1 | B. | 9x+3-10x-1=1 | C. | 9x+3-10x-1=12 | D. | 9x+3-10x+1=12 |
19.关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正.给出三个结论:①这两个方程的根都是负根;②(m-1)2+(n-1)2≥2;③-1≤2m-2n≤1.其中正确结论的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
16.多项式49a3bc3+14a2b2c2在分解因式时应提取的公因式是( )
| A. | 7a3bc3 | B. | 7a2b2c2 | C. | 7ab2c2 | D. | 7a2bc2 |
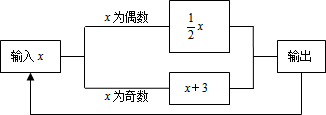 有一个程序机(如图),若输入4,则输出值是2,记作第一次操作;将2再次输入,则输出值是1,记作第二次操作…,则第2016次操作输出的数是4.
有一个程序机(如图),若输入4,则输出值是2,记作第一次操作;将2再次输入,则输出值是1,记作第二次操作…,则第2016次操作输出的数是4.