题目内容
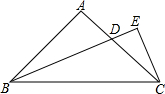 如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠ABE=∠EBC,CE⊥BD的延长线于E,求证:BD=2CE.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠ABE=∠EBC,CE⊥BD的延长线于E,求证:BD=2CE.考点:全等三角形的判定与性质
专题:证明题
分析:根据ASA推出△BEF≌△BEC,推出CE=FE=CF,求出∠ABD=∠ACF,∠BAD=∠CAF,根据ASA推出△ABD≌△ACF,推出BD=CF即可.
解答: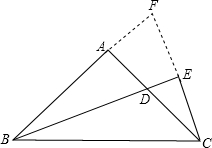 证明:延长BA交CE的延长线于F.
证明:延长BA交CE的延长线于F.
∵BE⊥CE,
∴∠BEF=∠BEC=90°,
在△BEF和△BEC中
∴△BEF≌△BEC(ASA),
∴CE=FE=
CF(全等三角形对应边相等),
∵∠BAC=90°,BE⊥CF,
∴∠BAD=∠CAF=90°,
∴∠BDA+∠ABD=∠EDC+∠ECA=90°
即∠ABD=∠ECA
在△ABD和△ACF中
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CE=EF=
CF,
∴BD=2CE.
 证明:延长BA交CE的延长线于F.
证明:延长BA交CE的延长线于F.∵BE⊥CE,
∴∠BEF=∠BEC=90°,
在△BEF和△BEC中
|
∴△BEF≌△BEC(ASA),
∴CE=FE=
| 1 |
| 2 |
∵∠BAC=90°,BE⊥CF,
∴∠BAD=∠CAF=90°,
∴∠BDA+∠ABD=∠EDC+∠ECA=90°
即∠ABD=∠ECA
在△ABD和△ACF中
|
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CE=EF=
| 1 |
| 2 |
∴BD=2CE.
点评:本题考查了全等三角形性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,已知的半径为R,C、D是直径AB同侧圆周上的两点,∠AOC=96°,∠BOD=36°,动点P在AB上,PC+PD的最小值是( )
如图,已知的半径为R,C、D是直径AB同侧圆周上的两点,∠AOC=96°,∠BOD=36°,动点P在AB上,PC+PD的最小值是( )| A、2R | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点. 如图,AB是⊙O的弦,四边形ABCD为正方形,DM是⊙O切线,M为切点,AB=2,DM=
如图,AB是⊙O的弦,四边形ABCD为正方形,DM是⊙O切线,M为切点,AB=2,DM=