题目内容
 如图,AB是⊙O的弦,四边形ABCD为正方形,DM是⊙O切线,M为切点,AB=2,DM=2
如图,AB是⊙O的弦,四边形ABCD为正方形,DM是⊙O切线,M为切点,AB=2,DM=2| 2 |
考点:切线的性质,正方形的性质
专题:
分析:延长DA交⊙O于N,连接BN,利用切割线定理可求出DN的长,进而得到AN的长,再利用圆周角定理可求出BN为圆的直径.利用勾股定理求出BN的长,即可得到圆的半径.
解答:解:延长DA交⊙O于N,连接BN,
∵DM是⊙O切线,
∴DM2=DA•DN,
∵DM=2
,
∴(2
)2=DA•DN,
∴DN=4,
∴AN=2,
∴AB=AN,
∵四边形ABCD为正方形,
∴∠NAB=90°,
∴BN是⊙O的直径,
∴BN=
=2
∴⊙O的半径
.

∵DM是⊙O切线,
∴DM2=DA•DN,
∵DM=2
| 2 |
∴(2
| 2 |
∴DN=4,
∴AN=2,
∴AB=AN,
∵四边形ABCD为正方形,
∴∠NAB=90°,
∴BN是⊙O的直径,
∴BN=
| 22+22 |
| 2 |
∴⊙O的半径
| 2 |
点评:本题考查了切割线定理,正方形的性质,圆周角定理以及勾股定理的运用,题目的综合性很好,难度中等,是一道不错的中考题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
下列运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、4
|
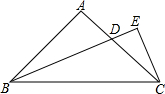 如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠ABE=∠EBC,CE⊥BD的延长线于E,求证:BD=2CE.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠ABE=∠EBC,CE⊥BD的延长线于E,求证:BD=2CE.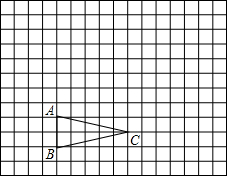 如图,△ABC在方格纸中.
如图,△ABC在方格纸中.