��Ŀ����
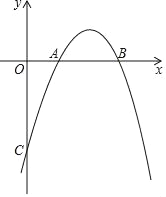
����Ŀ����֪�����κ���y=��x2+bx+c��ͼ����x�����������A��B�ĺ�����ֱ�Ϊ1��2����y��Ľ�����C��
��1����������κ����ı���ʽ��
��2������D��y���ϵ�һ�㣬�Ƿ����D��ʹ��B��C��DΪ���������������ABC���ƣ������ڣ����D�����꣬�������ڣ���˵�����ɣ�
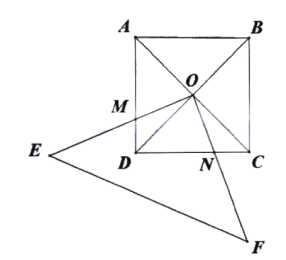
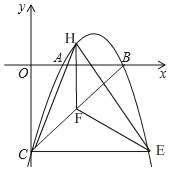
��3������C��CE��x�ᣬ����κ���y=��x2+bx+c��ͼ���ཻ�ڵ�E����H�Ǹö��κ���ͼ���ϵĶ��㣬����H��HF��y�ᣬ���߶�BC�ڵ�F����̽������H�˶����δ�ʱ����CHF����HFE�����֮��������H�����꼰��������
���𰸡���1�����κ����ı���ʽy=��x2+3x��2����2��D��0����1����D��0��6������3��������Ϊ1.5��H��1��0����
�������������������1������֪���ô���ϵ����������⼴�ɵý���ʽ��
��2��������������������������εı���ʽ���������D�����ꣻ
��3�������ֱ��BC�Ľ���ʽ�����������CHF���HFE�����֮�͵ĺ�����ϵʽ������������ֵ.
�����������1���߶��κ���y=��x2+bx+c��ͼ����x�����������A��B�ĺ�����ֱ�Ϊ1��2��
��A��1��0����B��2��0����
��![]() ��
��
��![]() ��
��
����κ����ı���ʽy=��x2+3x��2��
��2���߶��κ����ı���ʽy=��x2+3x��2��
��C��0����2����
��OC=2��
��A��1��0����B��2��0��
��OB=2��
��OB=OC��
���OBC=��OCB=45�㣬
���BAC��135�㣬������Dֻ���ڵ�C�Ϸ���y���ϣ�
���DCB=��ABC=45��
����D��0��d����d����2��
��A��1��0����B��2��0����C��0����2����
��AB=1��BC=2![]() ��CD=d+2��
��CD=d+2��
����B��C��DΪ��������������ABC���ƣ�
��١�DCB�ס�ABC��
��![]() =1��
=1��
��CD=AB=1��
��d+2=1��
��d=��1��
��D��0����1����
�ڡ�BCD�ס�ABC��
��![]() ��
��
��![]() ��
��
��d=6��
��D��0��6����
��3����ͼ��
��CE���ᣬ
����y=��2��
�ੁ2=��x2+3x��2��
��x=0���ᣩ��x=3��
��E��3����2����
��B��2��0����C��0����2����
��ֱ��BC�Ľ���ʽΪy=x��2����H��m����m2+3m��2����F��m��m��2����
�ߵ�F���߶�BC�ϵĵ㣬
��0��m��2��HF=��m2+3m��2����m��2��=��m2+2m��
��S��CHF+S��EHF=![]() HF��3=
HF��3=![]() ����m2+2m��=��
����m2+2m��=��![]() ��m2��2m+1��+
��m2��2m+1��+![]() =��
=��![]() ��m��1��2+
��m��1��2+![]() ��
��
��m=1ʱ����CHF���HFE�����֮�����������Ϊ![]() ����ʱ��H��1��0����
����ʱ��H��1��0����

 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�