Question

【题目】平面直角坐标系中，A是y＝﹣（x＞0）图象上一点，B是x轴正半轴上一点，点C的坐标为（0，﹣2），若点D与A，B，C构成的四边形为正方形，则点D的坐标_____．

Answer 1

【答案】（4，﹣2）或（2，﹣4）或（2﹣2，2﹣2）．

【解析】

首先依据题意画图图形，对于图1和图2依据正方形的对称性可得到点D的坐标，对于图3可证明△AEC≌△BFA，从而可得到AE=BF，然后由反比例函数的解析式可求得点A的坐标，然后可得到点D的坐标．

如图1所示：当CD为对角线时．

∵OC＝2，AB＝CD＝4，

∴D（4，﹣2）．

如图2所示：

∵OC＝2，BD＝AC＝4，

∴D（2，﹣4）．

如图3所示：过点A作AE⊥y轴，BF⊥AE，则△AEC≌△BFA．

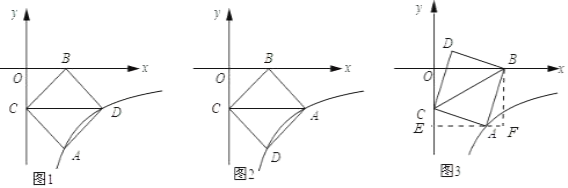
∴AE＝BF．

设点A的横纵坐标互为相反数，

∴A（2，﹣2）

∴D（2﹣2，2﹣2）．

综上所述，点D的坐标为（4，﹣2）或（2，﹣4）或（2﹣2，2﹣2）．

故答案为：（4，﹣2）或（2，﹣4）或（2﹣2，2﹣2）．