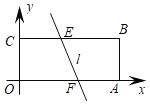题目内容
【题目】如图,正方形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,直角三角形
,直角三角形![]() 绕点
绕点![]() 按逆时针旋转,
按逆时针旋转,![]()
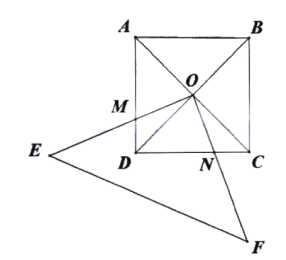
(1)若直角三角形绕点![]() 逆时针转动过程中分别交
逆时针转动过程中分别交![]() 两边于
两边于![]() 两点
两点
①求证:![]() ;
;
②连接![]() ,那么
,那么![]() 有什么样的关系?试说明理由
有什么样的关系?试说明理由
(2)若正方形的边长为2,则正方形![]() 与
与![]() 两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
【答案】(1)①见解析;②![]() 垂直且相等,理由见解析;(2)面积为1。
垂直且相等,理由见解析;(2)面积为1。
【解析】
(1)①证出△DOM≌∠CON,证出![]() ;
;
②证明△MDC≌△BCN得CM=BN,证明△GCN∽△MDC得BN⊥CM;
(2)因为△DOM≌∠CON,所以正方形![]() 与
与![]() 两个图形重叠部分为△DOC的面积.
两个图形重叠部分为△DOC的面积.
(1)①∵正方形![]() 的对角线
的对角线![]() 交于点
交于点![]()
∴∠ADO=∠ACD OD=OC ∠DOC=90°
②∵![]() ∠DOC=90°
∠DOC=90°
∴∠MOD+∠DON=90° ,∠NOD+∠CON=90°
∴∠DOM=∠CON
∵∠DOM=∠CON ∠ADO=∠ACD OD=OC
∴△DOM≌∠CON
∴![]()
②

设BN交CM于点G
∵正方形ABCD
∴DC=BC ∠ADC=∠DCB
∵△DOM≌∠CON
∴DM=CN
∴△MDC≌△BCN
∴CM=BN ∠CMD=∠BNC
∵∠CMD=∠BNC ∠MCD=∠MCD
∴△GCN∽△MDC
∴∠NGC=∠ADC
∴BN⊥CM
∴![]() 垂直且相等
垂直且相等
(2)面积为1.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据
月份n(月)1 | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.