��Ŀ����
����Ŀ����ͼ1���ı���ABCD��AEFG�����������غϵľ��Σ���ͼ2������AEFG�Ƶ�A��˳ʱ�뷽����ת���ȣ�0�ܦ���90�㣩����Gǡ�����ھ���ABCD�ĶԽ����ϣ�AB��FG�ཻ�ڵ�M������BE��FG�ڵ�N��
��1����AB=ADʱ����ֱ��д����ABE�Ķ�����
��2������ADB=60��ʱ������ABE�Ķ�����
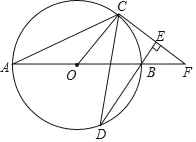
��3����ͼ3����AB=2AD=2ʱ�������A��ֱ��BE�ľ��룻 ��ֱ��д����BMN���ܳ���

���𰸡���1����ABE=45�㣻��2����ABE=60�㣻��3����A��ֱ��BE�ľ���Ϊ![]() ����BMN���ܳ�Ϊ=
����BMN���ܳ�Ϊ=![]() +
+![]() ��
��
��������
(1)��AB=ADʱ,�жϳ���G�͵�B�غ�,���ɵó�����;
(2) ���жϳ���ADG�ǵȱ�������, �ó���DAG=![]() , ���жϳ���ABE�ǵȱ�������, ���ɵó�����;
, ���жϳ���ABE�ǵȱ�������, ���ɵó�����;
(3)����ȷ����BD=![]() , sin��ADB=
, sin��ADB=![]() =
=![]() =COS��ABD, �����ó�AQ=
=COS��ABD, �����ó�AQ=![]() , ���жϳ���ADQ�צ�ABH, ���ɵó�����;
, ���жϳ���ADQ�צ�ABH, ���ɵó�����;
�������BH=![]() , ��: BE=2BH=
, ��: BE=2BH=![]() ���жϳ���FEN=��ABD, ���������BNM, ����ɦ�BMN�צ�BAE, ���M N=BM=
���жϳ���FEN=��ABD, ���������BNM, ����ɦ�BMN�צ�BAE, ���M N=BM=![]() , ���ɵó�����.
, ���ɵó�����.
�⣺��1����ͼ1��
��AB=ADʱ������ABCD�;���AEFG���������Σ�
����תʹ��G�������ζԽ�����ʱ����G�͵�B�غϣ�
����ABE�У���BAE=90�㣬AE=AB��
���ABE=45�㣻
��2����Rt��ABD�У���ADB=60�㣬
����ת֪��AD=AG��
���ADG�ǵȱ������Σ�
���DAG=60�㣬
���BAG=90�㩁60��=30�㣬
���BAE=90�㩁30��=60�㣬
��AB=AE��
���ABE�ǵȱ������Σ�
���ABE=60�㣻
��3������ͼ3��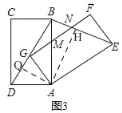
����A��AH��BE��H��
���BAH=![]() ��BAE��
��BAE��
��AH���ǵ�A��ֱ��BE�ľ��룬
��Rt��ABD��AB=2AD=2��
��AD=1�����ݹ��ɶ����ã�BD=![]() ��sin��ADB=
��sin��ADB=![]() =
=![]() =
=![]() =cos��ABD��
=cos��ABD��
����A��AQ��BD��Q��
���DAQ=![]() ��DAG��
��DAG��
��Rt��ADQ��tan��ADB=![]() =
=![]() ��
��
��AQ=![]() AD=
AD=![]() ��
��
����ת֪����DAG=��BAE��
���DAQ=��BAH��
�ߡ�AQD=��AHB��
���ADQ�ס�ABH��
��![]() =
=![]() ��
��
��AH=![]() ��
��
������A��ֱ��BE�ľ���Ϊ![]() ��
��
������֪��AH=![]() ��
��
��Rt��ABH�У����ݹ��ɶ����ã�BH=![]() =
=![]() ��
��
��BE=2BH=![]() ��
��
����֪����ABE=��ADB��
���NBG=90�㣬
�ߡ�NFE=90�㣬
���FEN=��BGN��
�ߡ�BGN+��QAG=90�㣬
���FEN=��GAQ=��DAQ=��ABD��
��Rt��EFN��cos��FEN=![]() =cos��ABD=
=cos��ABD=![]() ��
��
��![]() =
=![]() ��
��
��EN=![]() ��
��
��BN=BE��NE=![]() ��
��
��MN��AE��
���BMN�ס�BAE��
��![]() ��
��
��=![]()
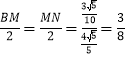 ��
��
��MN=BM=![]() ��
��
���BMN���ܳ�ΪMN+BM+BN=![]() ��
��

 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�����Ŀ��һ�����κ���ͼ���ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���
x | �� | ��4 | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | �� |
y | �� | �� | 0 |
| 2 |
| 0 | m | ��6 | �� | �� |
��1����������κ����ı���ʽ��
��2����m��ֵ��
��3���ڸ�����ֱ������ϵ�У��������������ͼ����
��4������ͼ��д����y��0ʱ��x��ȡֵ��Χ��