题目内容
10. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在直线上的C′处,得到经过点D的折痕DE.则$\frac{CE}{BE}$=$\sqrt{3}+1$.
如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在直线上的C′处,得到经过点D的折痕DE.则$\frac{CE}{BE}$=$\sqrt{3}+1$.
分析 如图,连接BD;首先证明∠C′DF=30°,∠C′=60°,进而得到∠DFC′=90°,此为解题的关键性结论;求出DF,进而求出BF;证明∠BEF=30°,得到BE=2BF,此为解题的又一关键性结论;求出CE,即可解决问题.
解答 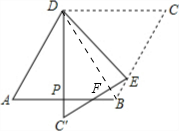 解:如图,连接BD,交C′E于点F;
解:如图,连接BD,交C′E于点F;
∵四边形ABCD为菱形,
∴DC∥AB,AB=AD;而∠A=60°,
∴△ABD为等边三角形,∠ADC=120°;
∴AD=BD,而AP=BP,
∴DP⊥AB,∠ADP=30°,
∴∠PDC=120°-30°=90°;
由题意得:∠C′DE=∠CDE=45°,
∠ADB=∠C′DB=60°,∠C′=∠C;
∴∠C′DF=90°-60°=30°;
∵四边形ABCD为菱形,
∴∠A=∠C,AD=DC=BC(设为λ);
∵∠C′=∠C,DC′=DC,
∴∠C′=60°,DC′=λ,
∴∠DFC′=90°,cos30°=$\frac{DF}{DC′}$,
∴DF=$\frac{\sqrt{3}}{2}$λ,BF=λ(1-$\frac{\sqrt{3}}{2}$);
在△DCE中,
∵∠DEC=180°-45°-60°=75°,
∴∠DEC′=∠DEC=75°,
∴∠BEF=180°-2×75°=30°,
∴BE=2BF=2λ-$\sqrt{3}$λ,
∴CE=λ-$(2λ-\sqrt{3}λ)$
=($\sqrt{3}-1$)λ,
∴$\frac{CE}{BE}$=$\frac{(\sqrt{3}-1)λ}{(2-\sqrt{3})λ}=\sqrt{3}+1$,
故答案为$\sqrt{3}$+1.
点评 该题主要考查了翻折变换的性质、菱形的性质、等腰三角形等几何知识点及其应用问题;解题的方法是作辅助线,构造直角三角形,将分散的条件集中;解题的关键是灵活运用翻折变换的性质、菱形的性质等知识点来分析、判断、解答.

 高中必刷题系列答案
高中必刷题系列答案| A. | 2.2×10-5千克 | B. | 2.2×10-6千克 | C. | 2.17×10-5千克 | D. | 2.17×10-6千克 |
| A. | 2 | B. | 3 | C. | 3.5 | D. | 4 |
| A. | 9:48-9:49 | B. | 9:49-9:50 | C. | 9:50-9:51 | D. | 9:51-9:52 |
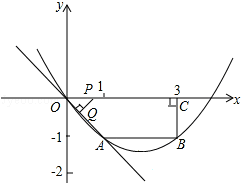 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.