题目内容
16. 如图所示,在平行四边形ABCD中,点E为DC中点,AE交BD于点O,且OD=3,求BD的长.
如图所示,在平行四边形ABCD中,点E为DC中点,AE交BD于点O,且OD=3,求BD的长.
分析 由平行四边形的性质可知,AB∥CD,则△AOB∽△EOD,根据相似三角形的性质得到$\frac{OD}{OB}=\frac{DE}{AB}$,代入数据即可得到结论.
解答 解:∵在?ABCD中,E为CD中点,
∴AB=CD=2DE,
又∵AB∥CD,
∴△AOB∽△EOD,
∴$\frac{OD}{OB}=\frac{DE}{AB}$,
即$\frac{3}{OB}=\frac{1}{2}$,
∴OB=6,
∴BD=OD+OB=9.
点评 此题考查了平行四边形的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
6. 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.
(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
(3)根据图象说明:当x为何值时,函数y随着x的增大而增大?当x为何值时,函数y随着x的增大而减小?
 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
| x | … | … | |||||
| y | … | … |
11. 已知有理数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知有理数a,b在数轴上的位置如图所示,下列结论错误的是( )
 已知有理数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知有理数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | -b<a<-1 | B. | 1<-a<b | C. | 1<|a|<b | D. | |a|<1<|b| |
1.已知A,B,C在一条直线上,AB=10,AC=6,那么AB的中点与AC的中点的距离为( )
| A. | 8 | B. | 2或8 | C. | 2 | D. | 6 |
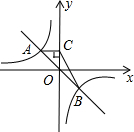 如图.函数y=-kx(k>0)与y=-$\frac{4}{x}$的图象交于A、B两点,过点A作AC垂直于y轴于点C,求△ABC的面积.
如图.函数y=-kx(k>0)与y=-$\frac{4}{x}$的图象交于A、B两点,过点A作AC垂直于y轴于点C,求△ABC的面积. 如图所示是小明家与周围地区的行走路线示意图,对小明家来说:
如图所示是小明家与周围地区的行走路线示意图,对小明家来说: