Question

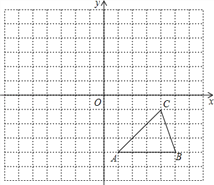
【题目】已知抛物线y＝x2+（m+1）x﹣m﹣2（m＞0）与x轴交于A、B两点，与y轴交于点C，不论m取何正数，经过A、B、C三点的⊙P恒过y轴上的一个定点，则该定点的坐标是_____．

Answer 1

【答案】(0,1)

【解析】

由题意根据已知条件得到求出OA=2，OB=m+2，OC=m+2，判断出∠OCB=∠OAF，根据三角函数的定义即可得到结论．

解：令y＝0，

∴x2+（m+1）x﹣m﹣2＝0，

∴（x﹣1）[x+（m+2）]＝0，

∴x＝1或x＝﹣（m+2），

∴A（1，0），B（﹣2，0），

∴OA＝1，OB＝m+2，

令x＝0，

∴y＝﹣m﹣2，

∴C（0，﹣m﹣2），

∴OC＝m+2，

如图，

∵点A，B，C在⊙P上，

∴∠OCB＝∠OAF，

在Rt△BOC中，tan∠OCB＝＝＝1，

在Rt△AOF中，tan∠OAF＝＝＝1，

∴OF＝1，

∴点F的坐标为（0，1）；

故答案为：（0，1）．