题目内容

19．如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律．则第（7）个图形中面积为1的正方形的个数为（　　）
A．20B．27C．35D．40

分析 第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的图象有2+3=5个，第（3）个图形中面积为1的正方形有2+3+4=9个，…，按此规律，第n个图形中面积为1的正方形有2+3+4+…+n+1=$\frac{n（n+3）}{2}$，进而可求出第（7）个图形中面积为1的正方形的个数．

解答 解：
第（1）个图形中面积为1的正方形有2个，
第（2）个图形中面积为1的图象有2+3=5个，
第（3）个图形中面积为1的正方形有2+3+4=9个，
…，
按此规律，
第n个图形中面积为1的正方形有2+3+4+…+（n+1）=$\frac{n（n+3）}{2}$，
当n=7时，图形中面积为1的正方形的个数=$\frac{70}{2}$=35，
故选C．

点评 此题考查图形的变化规律，找出图形与数字之间的运算规律，利用规律解决问题．

练习册系列答案
相关题目
9．最近，“雾霾天气”成为热门事件之一，霾对人类的危害巨大，大部分有害物质都富集在细微颗粒物PM2.5上，PM2.5是指直径小于或等于2.5微米的颗粒物，2.5微米即0.0000025米，把0.0000025用科学记数法表示为（　　）
A．0.25×10-5B．2.5×10-5C．2.5×10-6D．25×10-7
10．若4x2-9=0，则x的值是（　　）
A．±$\frac{3}{2}$B．$\frac{3}{2}$C．-$\frac{3}{2}$D．$\frac{9}{4}$
7．下列计算正确的是（　　）
A．（-p2q）3=-p5q3B．（12a2b3c）÷（6a2b）=2ab
C．（x-y）2=x2-y2D．a3•a4=a7
14．某中学为了培养学生的社会实践能力，今年“五一”长假期间要求学生参加一项社会调查活动．为此，小明在他所居住小区的600个家庭中，随机调查了50个家庭在日常开支（月消费）情况，并绘制了如下的频数分布表和频数分布直方图（收入取整数，单位：元）．
分 组频 数频 率
1000～120030.060
1200～1400120.240
1400～1600180.360
1600～18000.200
1800～20005
2000～22000.040
合计501.000
根据以上信息，如下结论错误的是（　　）
A．在1800～2000小组中的频率是0.1．
B．在 1600～1800小组中的频数是10．
C．被调查50个家庭个家庭中日常开支（月消费）低于1600元有33户．
D．估算该小区600个家庭中日常开支（月消费）较高（超过1800元）的家庭个数大约有7户．
4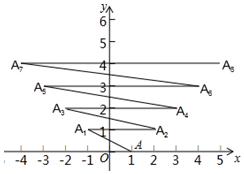．如图，点A（1，0）第一次跳动至点A1（-1，1），第二次跳动至点A2（2，1），第三次跳动至点A3（-2，2），第四次跳动至点A4（3，2），…，依此规律跳动下去，点A第102次跳动至点A102的坐标是（　　）
A．（-50，50）B．（-51，51）C．（52，51）D．（51，50）
11．计算：-8+（-6）=-14．
8．各顶点都在格点上的三角形叫格点三角形，如图，在4×8的方格中，以M、N为顶点且与△ABC相似的格点三角形的个数共有（　　）个．
A．3B．4C．5D．6
9．如图，数轴上A、B两点分别对应实数a、b，则下列结论中正确的是（　　）
A．a+b＞0B．ab＞0C．$\frac{|a|}{a}$+$\frac{|b|}{b}$=0D．a+ab-b＜0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网