Question

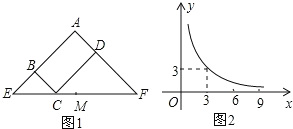
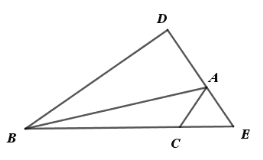
【题目】如图，△ABC中，AB=8，AC=2，∠BAC的外角平分线交BC延长线于点E，BD⊥AE于D，若AE=AC，则AD的长为______．

Answer 1

【答案】3

【解析】

延长AD至点G，使DG=AD，连接BG，延长BA至F，根据垂直平分线的性质可得BA=BG=8，然后根据等边对等角、角平分线的定义和平行线的判定证出AC∥GB，从而得出∠ACE=∠GBE，再根据等边对等角和等角对等边可证GB=GE=8，最后根据DG＋AD=GE－AE即可求出结论．

解：延长AD至点G，使DG=AD，连接BG，延长BA至F

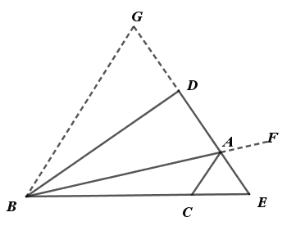
∴BD垂直平分AG

∴BA=BG=8

∴∠BAG=∠G

∵∠BAG=∠EAF，∠BAC的外角平分线交BC延长线于点E，

∴∠EAF=∠G，∠CAE=∠EAF，

∴∠G=∠CAE

∴AC∥GB

∴∠ACE=∠GBE

∵AE=AC=2

∴∠ACE=∠E

∴∠GBE=∠E

∴GB=GE=8

∵DG＋AD=GE－AE

∴2AD=6

∴AD=3

故答案为3．