题目内容
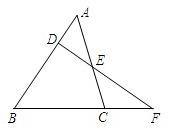24、如图，已知，D、E分别是△ABC的边AB、AC上的点，DE交BC的延长线于F，∠B=67°，∠ACB=74°，∠AED=48°，求∠F和∠BDF的度数．分析：根据对顶角相等可知∠CEF=∠AED；又∠ACB是△CEF的外角，所以根据外角的性质求出∠F； 根据三角形内角和定理可求∠BDF的度数．
解答：解：∵∠CEF=∠AED=48°，∠ACB=∠CEF+∠F，
∴∠F=∠ACB-∠CEF=74°-48°=26°；
∵∠BDF+∠B+∠F=180°，
∴∠BDF=180°-∠B-∠F
=180°-67°-26°
=87°．（4分）
∴∠F=∠ACB-∠CEF=74°-48°=26°；
∵∠BDF+∠B+∠F=180°，
∴∠BDF=180°-∠B-∠F
=180°-67°-26°
=87°．（4分）
点评：此题考查三角形内角和定理和三角形的外角的性质，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知：D、E分别是△ABC的AB、AC边上的点，且DE不与BC平行，能够判定△ABC∽△AED的条件是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，已知：D、E分别是△ABC的AB、AC边上一点，DE∥BC，若AD：AB=1：2，则S△ADE：S四边形BDEC=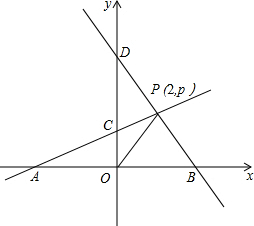
如图，已知：A、B分别是x轴上位于原点左、右两侧的点，点P（2，p）在第一象限，直线PA交y轴于点C（0，2），直线PB交y轴于点D，此时，S△AOP=6．