题目内容
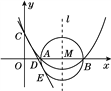
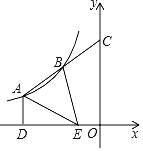
【题目】如图，△ABE中，点A、B是反比例函数y＝
（k≠0）图象上的两点，点E在x轴上，延长线段AB交y轴于点C，点B恰为线段AC中点，过点A作AD⊥x轴于点D．若S△ABE＝
，DE＝2OE，则k的值为（ ）
A.6B.﹣6C.9D.﹣9
【答案】B
【解析】
根据题意设A(2a，b)，则B(a，2b)，E(
，0)，作BM⊥x轴于M，根据S△ABE＝S梯形ABMD+S△BME﹣S△ADE，得出﹣
ab＝
，求得ab=-3，即可求出k＝2ab＝﹣6．
解：∵点A、B是反比例函数y＝
（k≠0）图象上的两点，点B恰为线段AC中点，
∴设A(2a，b)，则B(a，2b)，
∴k＝2ab，
∵DE＝2OE，
∴E(，0)，
作BM⊥x轴于M，
∵S△ABE＝S梯形ABMD+S△BME﹣S△ADE，S△ABE＝，
∴
(﹣a)(b+2b)+ (﹣a)2b﹣(﹣2a)b＝，
整理得﹣ab＝，
解得ab＝﹣3，
∴k＝2ab＝﹣6．
故选：B．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
