题目内容
△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,若∠DAE=26°,则∠BAC=
77
77
°.分析:作出图形,根据线段垂直平分线上的点到线段两端点的距离相等可得DA=DB,EA=EC,再根据等边对等角的性质可得∠DAB=∠B,∠EAC=∠C,然后利用三角形的内角和等于180°列式进行计算即可得解.
解答: 解:如图,∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
解:如图,∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠B+∠C=∠BAC+∠DAE,
在△ABC中,∠BAC+∠B+∠C=180°,
即∠BAC+∠BAC+∠DAE=180°,
∵∠DAE=26°,
∴2∠BAC=154°,
解得∠BAC=77°.
故答案为:77.
 解:如图,∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
解:如图,∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠B+∠C=∠BAC+∠DAE,
在△ABC中,∠BAC+∠B+∠C=180°,
即∠BAC+∠BAC+∠DAE=180°,
∵∠DAE=26°,
∴2∠BAC=154°,
解得∠BAC=77°.
故答案为:77.
点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,三角形的内角和定理,把∠B+∠C转化为∠BAC与∠DAE的和是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
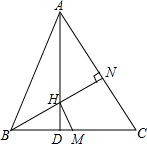 在△ABC中,H为垂心,M为BC上的中点,AD为BC上的高,且AD=BC(AC>AB).求证:HD+HM=MC.
在△ABC中,H为垂心,M为BC上的中点,AD为BC上的高,且AD=BC(AC>AB).求证:HD+HM=MC.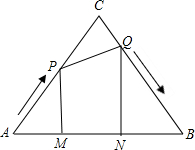 如图,等边三角形ABC的边长为8cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、N.
如图,等边三角形ABC的边长为8cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、N. 如图△ABC中,AB=AC,D是BC辺的中点,DE⊥AB,DF⊥AC,E,F为垂点.请你写出图中所有相等的线段,并说明理由.
如图△ABC中,AB=AC,D是BC辺的中点,DE⊥AB,DF⊥AC,E,F为垂点.请你写出图中所有相等的线段,并说明理由. 如图,点P在三角形ABC的边BC上.
如图,点P在三角形ABC的边BC上.