题目内容
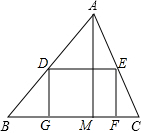如图，△ABC是一块锐角三角形余料，AM⊥BC，BC=10，AM=6，要把它加工成两邻边：| DE |
| DG |
| 5 |
| 3 |
考点：相似三角形的应用
专题：
分析：首先根据四边形DEFG是矩形证得△ADE∽△ABC，从而得到AN：AM=DE：BC，然后根据
=
，设DE=5x，则DG=NM=3x，从而得到（6-3x）：6=5x：10，求得x后即可求得周长．
| DE |
| DG |
| 5 |
| 3 |
解答：
解：∵四边形DEFG是矩形，
∴DE∥BC，
∴△ADE∽△ABC，
∴AN：AM=DE：BC，
∵
=
，
∴设DE=5x，则DG=NM=3x，
∴AN=6-3x，
∴（6-3x）：6=5x：10
解得：x=1，
∴周长为2（DE+DG）=2×（5x+3x）=16．
解：∵四边形DEFG是矩形，∴DE∥BC，
∴△ADE∽△ABC，
∴AN：AM=DE：BC，
∵
| DE |
| DG |
| 5 |
| 3 |
∴设DE=5x，则DG=NM=3x，
∴AN=6-3x，
∴（6-3x）：6=5x：10
解得：x=1，
∴周长为2（DE+DG）=2×（5x+3x）=16．
点评：本题考查了相似三角形的应用，解题的关键是能够从实际问题中抽象出相似三角形，难度不大．
练习册系列答案
相关题目
如图所示，有一块边长为24m的正方形绿地，绿地周边是小路，在绿地旁边的B处有健身器材，BC=7m．请你算一算，如果居住在A处的居民为了走近路而不惜践踏草地直接从A到B，这样比沿着绿地周边的小路，仅少走多少米？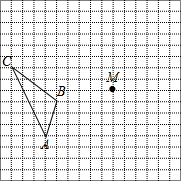
如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点M．