题目内容
设等边三角形的边长为x(x>0),面积为y,则y与x的函数关系式是
- A.y=
 x2
x2 - B.y=
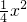
- C.y=
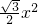
- D.y=

D
分析:作出三角形的高,利用直角三角形的性质及勾股定理可得高,利用三角形的面积= 底×高,把相关数值代入即可求解.
底×高,把相关数值代入即可求解.
解答: 解:作出BC边上的高AD.
解:作出BC边上的高AD.
∵△ABC是等边三角形,边长为x,
∴CD= x,
x,
∴高为h= x,
x,
∴y= x×h=
x×h= x2.
x2.
故选:D.
点评:此题主要考查了三角形的面积的求法,找到等边三角形一边上的高是难点,求出三角形的高是解决问题的关键.
分析:作出三角形的高,利用直角三角形的性质及勾股定理可得高,利用三角形的面积=
 底×高,把相关数值代入即可求解.
底×高,把相关数值代入即可求解.解答:
 解:作出BC边上的高AD.
解:作出BC边上的高AD.∵△ABC是等边三角形,边长为x,
∴CD=
 x,
x,∴高为h=
 x,
x,∴y=
 x×h=
x×h= x2.
x2.故选:D.
点评:此题主要考查了三角形的面积的求法,找到等边三角形一边上的高是难点,求出三角形的高是解决问题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
设等边三角形的边长为x(x>0),面积为y,则y与x的函数关系式是( )
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
 边形DEFG即为所求.
边形DEFG即为所求. x2
x2

