题目内容
求证：不论a取何值，2a2-a+1的值总是一个正数．
解：原式=2（a2-
a+
-）+1=2（a-）2+
∵（a-）2≥0
∴（a-）2+＞0
∴不论a取何值，2a2-a+1的值总是一个正数．
分析：把代数式变形为完全平方加正数的形式后即可判断．
点评：本题考查了配方法的应用及非负数的性质，难度一般，关键是正确变形为完全平方的形式后进行判断．
a+-）+1=2（a-）2+∵（a-
）2≥0∴（a-
）2+＞0∴不论a取何值，2a2-a+1的值总是一个正数．
分析：把代数式变形为完全平方加正数的形式后即可判断．
点评：本题考查了配方法的应用及非负数的性质，难度一般，关键是正确变形为完全平方的形式后进行判断．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
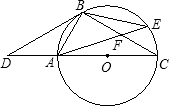本题为选做题，从甲、乙两题中选做一题即可，如果两题都做，只以甲题计分．