题目内容
 如图,点P是等边△ABC內任意一点,连接PA,PB,PC,过点C作CM,使CM=CP,∠BCM=∠ACP,连接BM.
如图,点P是等边△ABC內任意一点,连接PA,PB,PC,过点C作CM,使CM=CP,∠BCM=∠ACP,连接BM.(1)求证:△APC≌△BMC;
(2)若点P在∠ACB的平分线上,则由线段PA,PB,PC构成的三角形是什么三角形?请说明理由.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等边三角形性质可得AC=BC,即可证明△APC≌△BMC;
(2)根据(1)结论可得AP=BM,易证△PCM为等边三角形,根据垂直平分线性质可得BP=BM,由线段PA,PB,PC构成的三角形是等腰三角形.
(2)根据(1)结论可得AP=BM,易证△PCM为等边三角形,根据垂直平分线性质可得BP=BM,由线段PA,PB,PC构成的三角形是等腰三角形.
解答:(1)证明:∵△ABC是等边△,
∴AC=BC,
在△APC和△BMC中,
,
∴△APC≌△BMC;(SAS)
(2)∵△APC≌△BMC,
∴AP=BM,
∵∠BCM=∠ACP,PC平分∠ACB,
∴∠PCM=60°,
∴△PCM是等边三角形,且BC是∠PCM平分线,
∴BC是PM垂直平分线,
∴PB=BM,
∴由线段PA,PB,PC构成的三角形是等腰三角形.
∴AC=BC,
在△APC和△BMC中,
|
∴△APC≌△BMC;(SAS)
(2)∵△APC≌△BMC,
∴AP=BM,
∵∠BCM=∠ACP,PC平分∠ACB,
∴∠PCM=60°,
∴△PCM是等边三角形,且BC是∠PCM平分线,
∴BC是PM垂直平分线,
∴PB=BM,
∴由线段PA,PB,PC构成的三角形是等腰三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△APC≌△BMC是解题的关键.

练习册系列答案
相关题目
 小华利用计算器计算时,发现计算器的显示屏上显示如图的计算结果,对这个结果用小数表示应该是
小华利用计算器计算时,发现计算器的显示屏上显示如图的计算结果,对这个结果用小数表示应该是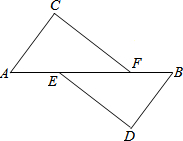 如图:A、E、F、B在一条直线上,下面四个条件:①AC=BD;②AE=BF;③AC∥BD;④∠C=∠D,请用其中三个作为条件,余下的一个作为结论,编一道数学问题,并写出解答过程.
如图:A、E、F、B在一条直线上,下面四个条件:①AC=BD;②AE=BF;③AC∥BD;④∠C=∠D,请用其中三个作为条件,余下的一个作为结论,编一道数学问题,并写出解答过程.