题目内容
9.已知二次函数y=ax2经过点A(-2,-8)(1)求二次函数的关系式;
(2)判断点B(-1,-4)是否在此抛物线上.
分析 (1)把A坐标代入解析式求出a的值,即可确定出解析式;
(2)把x=-1代入解析式求出y的值,即可做出判断.
解答 解:(1)把(-2,-8)代入二次函数解析式得:-8=4a,即a=-2,
则二次函数解析式为y=-2x2.
(2)不在,理由为:
把x=-1代入解析式得:y=-2,-2≠-4,
则点(-1,-4)步骤此抛物线上.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
20.下列四个数中,最小的数是( )
| A. | -2 | B. | 2 | C. | 0 | D. | -1 |
18.若函数$y=\frac{m}{x}$的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
| A. | m>1 | B. | m>0 | C. | m<1 | D. | m<0 |
19.已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )
| A. | sinA=$\frac{2}{3}$ | B. | cosA=$\frac{2}{3}$ | C. | tanA=$\frac{2}{3}$ | D. | cotA=$\frac{2}{3}$ |
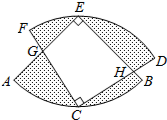 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为$\sqrt{2}$,则图中阴影部分的面积等于π-2.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为$\sqrt{2}$,则图中阴影部分的面积等于π-2.