题目内容
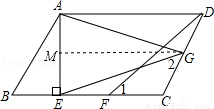
已知,如图,在 中,AE⊥ BC,垂足为E,点F为CE上的一点,点G为CD上的一点,CF=CG,连接DF、EG、AG, AG=EG,∠ 1=∠ 2.
中,AE⊥ BC,垂足为E,点F为CE上的一点,点G为CD上的一点,CF=CG,连接DF、EG、AG, AG=EG,∠ 1=∠ 2.

(1)若CE=4,AE=3,求BE的长;
(2)求证:∠CEG= ∠ AGE.
∠ AGE.
(1)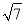 ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)根据所给的条件可证得△DFC≌△EGC,根据全等三角形的性质可得CD=CE=4,因为四边形ABCD是平行四边形,所以AB=CD=4, 在Rt△ABE中,由勾股定理求得BE即可;
(2)过G作GM⊥AE于点M,根据AE⊥BC,可得∠EMG=∠AEB=90°,所以GM∥BC, 根据平行的性质可得∠EGM=∠CEG,再有AG=EG,可得∠EGM=∠AGM= ∠AGE,所以∠CEG=
∠AGE,所以∠CEG= ∠AGE.
∠AGE.
试题解析:(1)【解析】
∵在△DFC和△EGC中,

∴△DFC≌△EGC(ASA),
∴CD=CE=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵AE⊥ BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=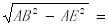
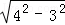 =
=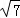 ;
;
(2)证明:过G作GM⊥AE于点M,
∵AE⊥BC,
∴∠EMG=∠AEB=90°,
∴GM∥BC,
∴∠EGM=∠CEG,
∵AG=EG,
∴∠EGM=∠AGM= ∠AGE
∠AGE
∴∠CEG= ∠AGE.
∠AGE.
考点:1.平行四边形的性质;2.三角形全等的判定和性质;3.勾股定理的应用;4.等腰三角形的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ﹣
﹣ )+3
)+3 = .
= . 的两实根,则
的两实根,则 的值为 .
的值为 .