题目内容
如图,从山顶A望地面上的C、D两点,测得它们的俯角分别是45°和30°,已知CD=100m,D、C、B在同一直线上,则山高AB=( )
A、100m B、50m C、50m D、50(+1)m
D
解析考点:解直角三角形的应用-仰角俯角问题.
分析:直角△ABC与直角△ABD有公共边AB,若设AB=x,则在直角△ABC与直角△ABD就满足解直角三角形的条件,可以用x表示出BC与BD的长,根据BD-BC=CD,即可列方程求解.
解答:解:设AB=x米,在直角△ACB中,∠ACB=45°,
∴BC=AB=x米.
在直角△ABD中,∠D=30°,tan∠D="AB/" BD ,
∴BD="AB/" tan30° =  x.
x.
∵BD-BC=CD
∴  x-x=100
x-x=100
解得:x=50( +1).
+1).
故选D.
点评:本题主要考查了解直角三角形的方法,解决的关键是注意到两个直角三角形有公共的边,利用公共边表示其它的量,从而把问题转化为方程问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
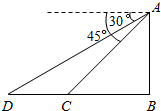 如图,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,点C在BD上,则山高AB=( )
如图,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,点C在BD上,则山高AB=( )| A、100米 | ||
B、50
| ||
C、50
| ||
D、50(
|
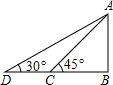 如图,从山顶A望地面C,D两点,俯角分别为45°,30°,若CD=100米,则山高AB为( )
如图,从山顶A望地面C,D两点,俯角分别为45°,30°,若CD=100米,则山高AB为( )| A、100米 | ||
B、50(
| ||
C、50
| ||
D、50
|
 如图,从山顶A望地面C、D两点,测得他们的俯角分别是45°和30°,已知CD=100米,点C位于BD上,求山AB的高度.(结果可保留根号)
如图,从山顶A望地面C、D两点,测得他们的俯角分别是45°和30°,已知CD=100米,点C位于BD上,求山AB的高度.(结果可保留根号) 如图,从山顶A望地面C、D两点,它们的俯角分别为30°、45°,若测得CD=100米,求AB的高度.(结果保留整数)
如图,从山顶A望地面C、D两点,它们的俯角分别为30°、45°,若测得CD=100米,求AB的高度.(结果保留整数)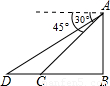
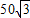 米
米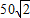 米
米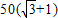 米
米