题目内容
 如图,从山顶A望地面C、D两点,测得他们的俯角分别是45°和30°,已知CD=100米,点C位于BD上,求山AB的高度.(结果可保留根号)
如图,从山顶A望地面C、D两点,测得他们的俯角分别是45°和30°,已知CD=100米,点C位于BD上,求山AB的高度.(结果可保留根号)
分析:设AB=xm,根据俯角的定义得到∠MAC=45°,∠MAD=30°,由平行线的性质得到∠D=30°,∠ACB=45°,再根据等腰三角形的性质得BC=AB=x,根据含30度的直角三角形三边的关系得DB=
AB,即100+x=
x,解出x即可.
| 3 |
| 3 |
解答:解:如图,设AB=xm,
∵∠MAC=45°,∠MAD=30°,
∴∠D=30°,∠ACB=45°,
在Rt△ABC中,BC=AB=x,
在Rt△ADB中,DB=CD+BC=100+x,
∴DB=
AB,即100+x=
x,解得x=50(
+1)m.
所以山AB的高度为50(
+1)米.
∵∠MAC=45°,∠MAD=30°,
∴∠D=30°,∠ACB=45°,
在Rt△ABC中,BC=AB=x,
在Rt△ADB中,DB=CD+BC=100+x,
∴DB=
| 3 |
| 3 |
| 3 |
所以山AB的高度为50(
| 3 |
点评:本题考查了解直角三角形的应用:向下看,视线与水平线的夹角叫俯角.也考查了等腰直角三角形和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
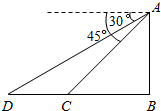 如图,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,点C在BD上,则山高AB=( )
如图,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,点C在BD上,则山高AB=( )| A、100米 | ||
B、50
| ||
C、50
| ||
D、50(
|
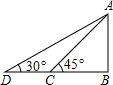 如图,从山顶A望地面C,D两点,俯角分别为45°,30°,若CD=100米,则山高AB为( )
如图,从山顶A望地面C,D两点,俯角分别为45°,30°,若CD=100米,则山高AB为( )| A、100米 | ||
B、50(
| ||
C、50
| ||
D、50
|
 如图,从山顶A望地面C、D两点,它们的俯角分别为30°、45°,若测得CD=100米,求AB的高度.(结果保留整数)
如图,从山顶A望地面C、D两点,它们的俯角分别为30°、45°,若测得CD=100米,求AB的高度.(结果保留整数)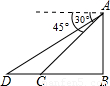
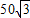 米
米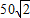 米
米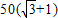 米
米