题目内容
11.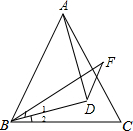 如图,D为等边△ABC内一点,DB=DA,BF=AB,∠1=∠2,则∠BFD的度数为( )
如图,D为等边△ABC内一点,DB=DA,BF=AB,∠1=∠2,则∠BFD的度数为( )| A. | 15o | B. | 20o | C. | 30o | D. | 45o |
分析 连接DC,证明△BDF≌△BDC≌△ACD后,根据全等三角形的对应角相等进行求解.
解答 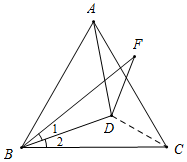 解:连接DC.
解:连接DC.
∵等边三角形ABC,
∴AB=BC=AC,
∵AB=BF,
∴BF=AB=BC,
在△FBD和△CBD中,
$\left\{\begin{array}{l}{BF=BC}\\{∠1=∠2}\\{BD=BD}\end{array}\right.$,
∴△FBD≌△CBD(SAS),
∴∠BFD=∠BCD,
在△ACD和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{CD=CD}\\{BD=AD}\end{array}\right.$,
∴△ACD≌△BCD(SSS),
∴∠ACD=∠BCD,
∵∠ACB=60°,
∴∠ACD=∠BCD=∠BFD=30°.
故选:C.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
相关题目
2.方程(x-1)(x+2)=2(x+2)的根是( )
| A. | 1,-2 | B. | 3,-2 | C. | 0,-2 | D. | 1,2 |
1.如果将抛物线y=(x-1)2+2向下平移1个单位,那么所得的抛物线解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x-1)2+1 | C. | y=(x-2)2+2 | D. | y=x2+2 |
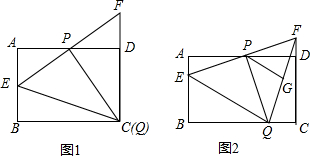
 如图,△ABD≌△ACE,如果BE=3cm,AC=5cm,那么AD=2cm.
如图,△ABD≌△ACE,如果BE=3cm,AC=5cm,那么AD=2cm.