题目内容
正六边形的边长为1cm,则它的边心距为( )
A、
| ||||
| B、1cm | ||||
| C、2cm | ||||
D、
|
考点:正多边形和圆
专题:
分析:连接OA、OB,根据正六边形的性质求出∠AOB,得出等边三角形OAB,求出OA、AM的长,根据勾股定理求出即可.
解答: 解:连接OA、OB、OC、OD、OE、OF,
解:连接OA、OB、OC、OD、OE、OF,
∵正六边形ABCDEF,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,
∴∠AOB=360°÷6=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=1cm,
∵OM⊥AB,
∴AM=BM=
,
在△OAM中,由勾股定理得:OM=
=
(cm).
故选A.
 解:连接OA、OB、OC、OD、OE、OF,
解:连接OA、OB、OC、OD、OE、OF,∵正六边形ABCDEF,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,
∴∠AOB=360°÷6=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=1cm,
∵OM⊥AB,
∴AM=BM=
| 1 |
| 2 |
在△OAM中,由勾股定理得:OM=
| OA2-AM2 |
| ||
| 2 |
故选A.
点评:本题主要考查对正多边形与圆,勾股定理,等边三角形的性质和判定等知识点的理解和掌握,能求出OA、AM的长是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知:当x=1时,代数式
ax3-3bx+4的值是7,那么,当x=-1时,这个代数式的值是( )
| 1 |
| 2 |
| A、7 | B、3 | C、1 | D、-7 |
用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是( )
| A、圆锥 | B、球体 |
| C、圆柱 | D、以上都有可能 |
 如图,图形旋转一定角度后能与自身重合,则旋转的最小角度是( )
如图,图形旋转一定角度后能与自身重合,则旋转的最小角度是( )| A、45° | B、90° |
| C、180° | D、360° |
已知扇形的圆心角为120°,半径为6cm,则扇形的面积为( )
| A、12cm2 |
| B、36cm2 |
| C、12πcm2 |
| D、36πcm2 |
下列函数中是二次函数的是( )
| A、y=4x2+1 | ||
| B、y=4x+1 | ||
C、y=
| ||
D、y=
|
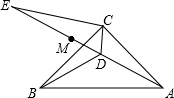 如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.