题目内容
口袋中有4个相同的小球,它们分别写有数字2、3、4、5,从口袋中随机的取出两个球,用所得的两个数a和b构成函数y=ax-2和y=x+b,则使这两个函数的交点在直线x=2右侧的概率等于________.

分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与使这两个函数的交点在直线x=2右侧的情况,再利用概率公式求解即可求得答案.
解答:画树状图得:

∵共有12种等可能的结果,使这两个函数的交点在直线x=2右侧的(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共6种情况,
∴使这两个函数的交点在直线x=2右侧的概率为:
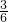 =
= .
.故答案为:
 .
.点评:此题考查的是用列表法或树状图法求概率与一次函数的交点问题.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
不透明的口袋中有2个白球和1个红球,球除颜色外其它都相同.摸球试验规定:摸出一个球后,要放回袋中,再进行下一次试验.小明摸了两次,均摸出了白球,则他第三次摸球的结果是( )
| A、一定是红球 | B、一定是白球 | C、红球的可能性较大 | D、白球的可能性较大 |
下列说法中,正确的是( )
A、口袋中有3个白球,2个黑球,1个红球,它们除颜色外都相同,因为袋中共有3种颜色的球,所以摸到红球的概率是
| ||
B、掷一枚硬币两次,可能的结果为两次都是正面,一次正面一次反面,两次都是反面,所以掷出两次都是反面的概率为
| ||
C、小明参加篮球投篮游戏,因为投篮一次,只有两种可能的结果,不是“投中”就是“未投中”,所以投中的概率为
| ||
D、掷一枚只有六个面骰子,合数点朝上的概率是
|