题目内容
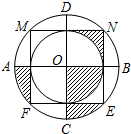 如图,正方形MNEF的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是
如图,正方形MNEF的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是π
π
.分析:由于正方形MNEF的四个顶点在大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则通过旋转得到图中阴影部分的面积等于正方形OHEQ的面积与弓形FCE的面积和,而正方形OHEQ的面积等于△OFE的面积,所以图中阴影部分的面积等于扇形OFE的面积,然后根据扇形面积公式计算即可.
解答:解: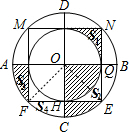 如图,
如图,
根据题意把正方形与小圆绕圆心O顺时针旋转90°,面积为S1的部分与面积为S2的部分重合,
把正方形与小圆绕圆心O逆时针旋转90°,面积为S3的部分与面积为S4的部分重合,
∴图中阴影部分的面积等于正方形OHEQ的面积与弓形FCE的面积和,
∵正方形OHEQ的面积等于△OFE的面积,
∴图中阴影部分的面积等于扇形OFE的面积,即图中阴影部分的面积=
=π.
故答案为π.
 如图,
如图,根据题意把正方形与小圆绕圆心O顺时针旋转90°,面积为S1的部分与面积为S2的部分重合,
把正方形与小圆绕圆心O逆时针旋转90°,面积为S3的部分与面积为S4的部分重合,
∴图中阴影部分的面积等于正方形OHEQ的面积与弓形FCE的面积和,
∵正方形OHEQ的面积等于△OFE的面积,
∴图中阴影部分的面积等于扇形OFE的面积,即图中阴影部分的面积=
| 90•π•22 |
| 360 |
故答案为π.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了切线的性质、正方形的性质和扇形的面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•娄底)如图,正方形MNEF的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是( )
(2012•娄底)如图,正方形MNEF的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是( )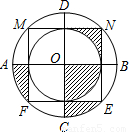
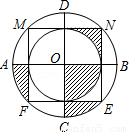
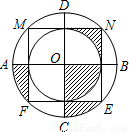 如图,正方形MNEF的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是( )
如图,正方形MNEF的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是( )