题目内容
 如图,PB、PC分别是△ABC的外角平分线,它们相交于点P,求证:点P在∠A的平分线上.
如图,PB、PC分别是△ABC的外角平分线,它们相交于点P,求证:点P在∠A的平分线上.
证明:作PM⊥AC于M,PN⊥BC于N,PE⊥AB于E,
∵PB、PC分别是△ABC的外角平分线,
∴PM=PN,PN=PE,
∴PM=PE,
∵PM⊥AC,PE⊥AB,
∴点P在∠A的平分线上.
分析:作PM⊥AC于M,PN⊥BC于N,PE⊥AB于E,根据角平分线性质得出PM=PN,PN=PE,推出PM=PE,根据角平分线性质推出即可.
点评:本题考查了角平分线性质的应用,注意:角平分线上的点到角两边的距离相等.

∵PB、PC分别是△ABC的外角平分线,
∴PM=PN,PN=PE,
∴PM=PE,
∵PM⊥AC,PE⊥AB,
∴点P在∠A的平分线上.
分析:作PM⊥AC于M,PN⊥BC于N,PE⊥AB于E,根据角平分线性质得出PM=PN,PN=PE,推出PM=PE,根据角平分线性质推出即可.
点评:本题考查了角平分线性质的应用,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 11、如图,PB,PC分别切⊙O于B、C两点,点A在⊙O上,若∠A=65°,则∠P=
11、如图,PB,PC分别切⊙O于B、C两点,点A在⊙O上,若∠A=65°,则∠P= 已知:如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P与AB垂直,求证:P是AD的中点.
已知:如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P与AB垂直,求证:P是AD的中点.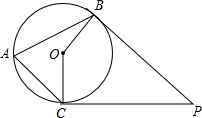 如图,PB,PC分别切⊙O于B、C两点,点A在⊙O上,若∠A=65°,则∠P=________.
如图,PB,PC分别切⊙O于B、C两点,点A在⊙O上,若∠A=65°,则∠P=________.