题目内容
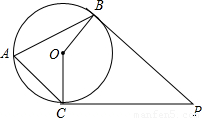
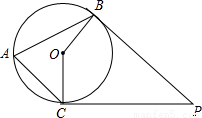
11、如图，PB，PC分别切⊙O于B、C两点，点A在⊙O上，若∠A=65°，则∠P=50°
．分析：先根据∠COB是∠CAB同弧所对的圆心角求出∠COB的度数，再根据CO⊥PC、PB⊥OB，在四边形PCOB中求出∠P的值．
解答：解：在⊙O中，∠COB=2∠CAB-130°
∵PB、PC是⊙O的切线
所以∠PBO=∠PCO=90°
在四边形PBOC中，
∠P=360°-∠COB-∠PBO-∠PCO=50°，
所以答案为50°．
∵PB、PC是⊙O的切线
所以∠PBO=∠PCO=90°
在四边形PBOC中，
∠P=360°-∠COB-∠PBO-∠PCO=50°，
所以答案为50°．
点评：本题综合考查了切线的性质，四边形内角和以及圆心角与对应圆周角的关系．
练习册系列答案
相关题目
已知：如图，AB∥CD，PB和PC分别平分∠ABC和∠DCB，AD过点P与AB垂直，求证：P是AD的中点．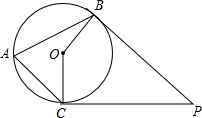
如图，PB，PC分别切⊙O于B、C两点，点A在⊙O上，若∠A=65°，则∠P=________．
