题目内容
已知 是方程x2-(3tanθ)x+
是方程x2-(3tanθ)x+ =0的一个根,θ是三角形的一个内角,那么cosθ的值为 .
=0的一个根,θ是三角形的一个内角,那么cosθ的值为 .
【答案】分析:将x= 代入已知方程,列出关于tanθ的值,然后根据特殊角的三角形函数值求得θ的数值.最后根据锐角θ来求cosθ的值
代入已知方程,列出关于tanθ的值,然后根据特殊角的三角形函数值求得θ的数值.最后根据锐角θ来求cosθ的值
解答:解:∵ 是方程x2-(3tanθ)x+
是方程x2-(3tanθ)x+ =0的一个根,
=0的一个根,
∴x= 满足方程x2-(3tanθ)x+
满足方程x2-(3tanθ)x+ =0,
=0,
∴( +1)2-(3tanθ)(
+1)2-(3tanθ)( +1)+
+1)+ =0,解得,tanθ=1.
=0,解得,tanθ=1.
∵θ是锐角,
∴θ=45°,
∴cosθ=
故答案是: .
.
点评:本题考查的是一元二次方程的根即方程的解的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.
 代入已知方程,列出关于tanθ的值,然后根据特殊角的三角形函数值求得θ的数值.最后根据锐角θ来求cosθ的值
代入已知方程,列出关于tanθ的值,然后根据特殊角的三角形函数值求得θ的数值.最后根据锐角θ来求cosθ的值解答:解:∵
 是方程x2-(3tanθ)x+
是方程x2-(3tanθ)x+ =0的一个根,
=0的一个根,∴x=
 满足方程x2-(3tanθ)x+
满足方程x2-(3tanθ)x+ =0,
=0,∴(
 +1)2-(3tanθ)(
+1)2-(3tanθ)( +1)+
+1)+ =0,解得,tanθ=1.
=0,解得,tanθ=1.∵θ是锐角,
∴θ=45°,
∴cosθ=

故答案是:
 .
.点评:本题考查的是一元二次方程的根即方程的解的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.

练习册系列答案
相关题目
 是方程x2-2x+c=0的一个根,则另一个根是 .
是方程x2-2x+c=0的一个根,则另一个根是 . 是方程x2-2x+c=0的一个根,则另一个根是 .
是方程x2-2x+c=0的一个根,则另一个根是 . 是方程x2-ay2-bx=0的两个解,那么ab= .
是方程x2-ay2-bx=0的两个解,那么ab= .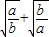 的值.
的值.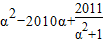 的值.
的值.