题目内容
已知关于x的一元二次方程x2-2xsinα+
sinα-
=0有两个相等的实数根，求锐角α的度数．
| 3 |
| 3 |
| 4 |
考点：根的判别式,特殊角的三角函数值
专题：
分析：因为方程有两个相等的实数根，则△=（2sinα）2-4（
sinα-
）=0，解关于sinα的方程，求出sinα的值，再据此求出α的值即可．
| 3 |
| 3 |
| 4 |
解答：解：∵关于x的一元二次方程x2-2xsinα+
sinα-
=0有两个相等的实数根，
∴△=（2sinα）2-4（
sinα-
）=0
解得sinα=
，
∴α=60°．
| 3 |
| 3 |
| 4 |
∴△=（2sinα）2-4（
| 3 |
| 3 |
| 4 |
解得sinα=
| ||
| 2 |
∴α=60°．
点评：此题考查一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
下列计算中，正确的是（ ）
| A、（0.01）0=0 |
| B、（-1）-1=1 |
| C、（10-5×2）0=1 |
| D、100=1 |
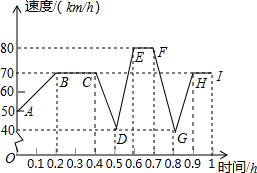平川四中教生物的王老师驱车到屈吴山采集植物标本，在上山行驶过程中，要经过上坡、下坡、平路等路段，她的SUV在自身动力不变的情况下，上坡时速度越来越慢，下坡时速度越来越快，平路上保持匀速行驶，下面的图象表示了她开车在山区行驶过程中的速度随时间变化的情况．