题目内容
如图,抛物线 交
交 轴于
轴于 两点(
两点( 的左侧),交
的左侧),交 轴于点
轴于点 ,顶点为
,顶点为 。
。

(1)求点 的坐标;
的坐标;
(2)求四边形 的面积;
的面积;
(3)抛物线上是否存在点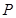 ,使得
,使得 ,若存在,请求出点
,若存在,请求出点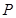 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
【答案】
(1) A(-1,0);B(3,0);C(0,3);(2)9;(3) 存在这样的点P,P点的坐标为(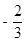 ,
,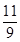 )或(
)或(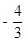 ,
,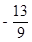 ).
).
【解析】
试题分析:(1)在抛物线的解析式中,令x=0可以求出点C的坐标,令x=0可以求出A、B点的坐标.
(2)过D作DE⊥AB,垂足为E,则四边形ABDC的面积就是: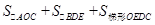
(3)根据条件判定△BCD是直角三角形,再依据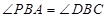 求出
求出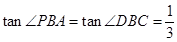 .设P点坐标为(m,-m2+2m+3),分两种情况讨论:(1)当P点在x 轴上方时,(2)当P点在x轴下方时,解直角三角形即可求出m的值,从而确定点P的坐标.
.设P点坐标为(m,-m2+2m+3),分两种情况讨论:(1)当P点在x 轴上方时,(2)当P点在x轴下方时,解直角三角形即可求出m的值,从而确定点P的坐标.
试题解析:(1)当x=0时,y=-x2+2x+3=3;
当y=0时,0=-x2
解得:x1=-1、x2=3;
故A(-1,0);B(3,0);C(0,3).
(2)
∴D点坐标为(1,4)
过点D作DE⊥x轴于E
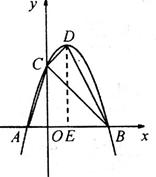
∴OE=1,DE=4
∴BE=OB-OE=2
∵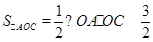 ,
, ,
,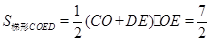
∴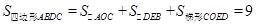
(3)假设存在这样的点P
过点C作CF⊥DE于F
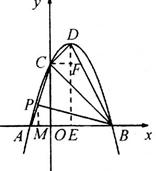
∴CF=1,DF=1
∴∠DCF=45°,CD=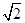
∵OC=3=OB,
∴∠CBO=45°,BC=
∵CF∥x轴
∴∠FCB=∠CBO=45°,
∴∠DCB=90°
在Rt△BCD中,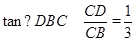
∴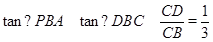
设P点坐标为(m,-m2+2m+3),
过点P作PM⊥AB于M
当P点在x轴上方时,PM=-m2+2m+3,BM=3-m
在Rt△PBM中,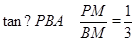 ,即
,即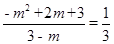
∴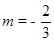 或
或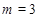 (舍去)
(舍去)
∴P点坐标为(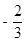 ,
,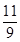 )
)
当P点在x轴下方时,PM=-m2-2m-3,BM=3-m
在Rt△PBM中,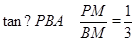 ,即
,即
∴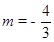 或
或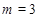 (舍去)
(舍去)
∴P点坐标为(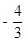 ,
,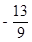 )
)
综上,存在这样的点P,P点的坐标为(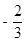 ,
,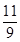 )或(
)或(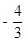 ,
,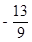 )
)
考点: 二次函数综合题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 轴交于
轴交于 (2)点
(2)点 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以 轴交于
轴交于 (
( ,0)、
,0)、 (
( ,0)两点,且
,0)两点,且 ,与
,与 轴交于点
轴交于点 ,其中
,其中 是方程
是方程 的两个根。
的两个根。 是线段
是线段 上的一个动点,过点
上的一个动点,过点 ∥
∥ ,交
,交 于点
于点 ,连接
,连接 ,当
,当 的面积最大时,求点
的面积最大时,求点 在(1)中抛物线上,点
在(1)中抛物线上,点 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点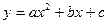 交
交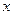 轴于
轴于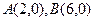 两点,交
两点,交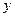 轴于点
轴于点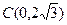 .
.
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线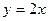 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交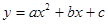 交
交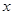 轴于
轴于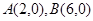 两点,交
两点,交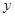 轴于点
轴于点 .
.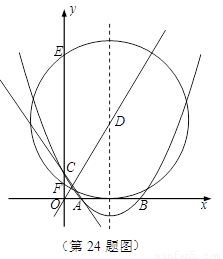
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线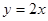 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交