题目内容
17．若x为27的立方根，y为9的平方根，则代数式x+y的值为6或0．分析 根据题意可以求得x、y的值，从而可以解答本题．
解答 解：x为27的立方根，y为9的平方根，
∴x=3，y=±3，
∴x+y=3+3=6，或x+y=3-3=0，
故答案为：6或0．
点评 本题考查立方根、平方根，解答本题的关键是明确它们各自的含义．
练习册系列答案
名校课堂系列答案
相关题目
有一容器的形状如图所示，现匀速地向该容器内注水，直到把容器注满，在注水过程中，容器内的水面高度h与注水时间t的大致图象为（ ）
6．（1）图（1）是正方体木块，把它切去一块，可能得到形如图（2），（3），（4），（5）的木块．
我们知道，图（1）的正方体木块有8个顶点，12条棱，6个面，请你将图（2），（3），（4），（5）中木块的顶点数，棱数，面数填入表：
（2）观察表，请你归纳上述各种木块的顶点数，棱数，面数之间的数量关系，这种数量关系是：
顶点数+面数-2=棱数．
（3）图⑥是用虚线画出的正方体木块，请你想象一种与图②～⑤不同的切法，把切去一块后得到的那一块的每条棱都改画成实线，则该木块的顶点数为8，棱数为12，面数为6．这与你（2）题中所归纳的关系是否相符？
我们知道，图（1）的正方体木块有8个顶点，12条棱，6个面，请你将图（2），（3），（4），（5）中木块的顶点数，棱数，面数填入表：
| 图 | 顶点数 | 棱数 | 面数 |
| （1） | 8 | 12 | 6 |
| （2） | 6 | 9 | 5 |
| （3） | 8 | 12 | 6 |
| （4） | 8 | 13 | 7 |
| （5） | 10 | 15 | 7 |
顶点数+面数-2=棱数．
（3）图⑥是用虚线画出的正方体木块，请你想象一种与图②～⑤不同的切法，把切去一块后得到的那一块的每条棱都改画成实线，则该木块的顶点数为8，棱数为12，面数为6．这与你（2）题中所归纳的关系是否相符？
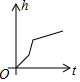
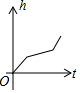
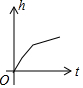
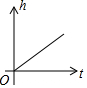
如图，P为矩形ABCD边上的一个动点，沿ABCD方向运动，P点运动的路程为x．△PAD的面积为y，则y与x的函数关系用图象表示大致是（ ）
