题目内容
7．将5个完全相同的小球装甲、乙两个不透明的口袋中，甲袋装3个，乙袋装2个，甲袋球标有数字2、3、4，乙袋标2、4，从两袋中各摸一球．（1）用列表法或树状法，求模出的数字之和为5的概率．
（2）摸出数字之和为多少时概率最大？
分析 （1）依据题意先用列表法或画树状图法分析所有等可能和达到某种效果的可能；
（2）然后根据概率公式求出该事件的概率．
解答 解：（1）画树形图得：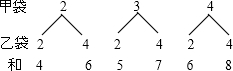
摸出的两个球上数字之和为5的概率为$\frac{1}{6}$．
（2）从表看，摸出的两个球上数字之和为8时概率最大．
点评 本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
12．当今，青少年视力水平的下降已引起全社会的关注，为了了解某中学毕业年级500名学生的视力情况，从中抽取了一部分学生做视力调查，对所得数据整理如下：
（1）填写频率分布表中未完成的部分；
（2）在这个问题中，样本是50名学生的视力情况；
（3）若视力为4.9、5.0、5.1均属正常，不需矫正，试估计该校毕业年级学生视力不正常的约为180人；
（4）若要较直观地表示出该校毕业年级学生视力的分布情况，还应绘制频数分布直方图．
| 分 组 | 频 数 | 频 率 |
| 3.95～4.25 | 2 | 0.04 |
| 4.25～4.55 | 6 | 0.12 |
| 4.55～4.85 | 23 | 0.46 |
| 4.85～5.15 | 18 | 0.36 |
| 5.15～5.45 | 1 | 0.02 |
| 合 计 | 1 |
（2）在这个问题中，样本是50名学生的视力情况；
（3）若视力为4.9、5.0、5.1均属正常，不需矫正，试估计该校毕业年级学生视力不正常的约为180人；
（4）若要较直观地表示出该校毕业年级学生视力的分布情况，还应绘制频数分布直方图．
19．设扇形的面积为49㎡，其弧长为14m，则其所在的圆的半径为（ ）
| A． | 21m | B． | 14m | C． | 7m | D． | $\frac{7}{2}$m |