题目内容
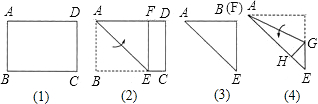
 将矩形纸片ABCD沿着对角线AC折叠,使点B落在点E处.
将矩形纸片ABCD沿着对角线AC折叠,使点B落在点E处.(1)EF和DF的大小关系如何?请说明理由.
(2)若∠ACB=20,求∠EAF的度数.
分析:(1)EF=DF,由折叠的性质得到三角形ABC与三角形AEC全等,再由矩形中三角形ABC与三角形ADC全等,得到三角形AEC与三角形ADC全等,得到∠DAC=∠ECA,利用等角对等边得到AF=CF,再由一对直角相等,一对对顶角相等,利用AAS得到三角形AEF与三角形CDF全等,即可得到EF=DF;
(2)在直角三角形ABC中,由∠ACB的度数,求出∠BAC的度数,进而求出∠EAC的度数,再由A与BC平行,利用两直线平行内错角相等得到∠DAC=∠ACB,由∠EAC-∠DAC即可求出∠EAF的度数.
(2)在直角三角形ABC中,由∠ACB的度数,求出∠BAC的度数,进而求出∠EAC的度数,再由A与BC平行,利用两直线平行内错角相等得到∠DAC=∠ACB,由∠EAC-∠DAC即可求出∠EAF的度数.
解答:解:(1)EF=DF,理由为:
由折叠的性质得到△ABC≌△AEC,再由矩形的性质得到△ABC≌△ADC,
∴△AEC≌△ADC,∠E=∠D=90°,
∴∠DAC=∠ECA,
∴AF=CF,
在△AEF和△CDF中,
,
∴△AEF≌△CDF(AAS),
则EF=DF;
(2)∵AD∥BC,
∴∠DAC=∠ACB=20°,
∵在Rt△ABC中,∠B=90°,∠ACB=20°,
∴∠BAC=∠EAC=60°,
则∠EAF=∠EAC-∠DAC=40°.
由折叠的性质得到△ABC≌△AEC,再由矩形的性质得到△ABC≌△ADC,
∴△AEC≌△ADC,∠E=∠D=90°,
∴∠DAC=∠ECA,
∴AF=CF,
在△AEF和△CDF中,
|
∴△AEF≌△CDF(AAS),
则EF=DF;
(2)∵AD∥BC,
∴∠DAC=∠ACB=20°,
∵在Rt△ABC中,∠B=90°,∠ACB=20°,
∴∠BAC=∠EAC=60°,
则∠EAF=∠EAC-∠DAC=40°.
点评:此题考查了翻折变换(折叠问题),涉及的知识有:全等三角形的判定与性质,矩形的性质,以及平行线的性质,熟练掌握折叠的性质是解本题的关键.

练习册系列答案
相关题目
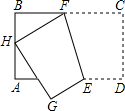 如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG=40°,则∠GEF的度数为( )
如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG=40°,则∠GEF的度数为( )| A、100° | B、110° | C、120° | D、135° |
 18、如图,将矩形纸片ABCD沿EF折叠后,点C、D分别落在点C′、D′处,若∠AFE=65°,则∠C′EF=
18、如图,将矩形纸片ABCD沿EF折叠后,点C、D分别落在点C′、D′处,若∠AFE=65°,则∠C′EF= 如图,将矩形纸片ABCD沿BD折叠,使点A落在点A′处,设A′B与CD相交于点E,若AB=8,BC=6,则EB=
如图,将矩形纸片ABCD沿BD折叠,使点A落在点A′处,设A′B与CD相交于点E,若AB=8,BC=6,则EB=