题目内容
△ABC的底边BC=48，高AD=16，E，H分别在AB，AC边上，F，G在BC边上，若EF：FG=5：9，求矩形EFGH的周长．
解：设EF=5x，则HE=9x，
∵矩形EFGH内接于△ABC且AD⊥BC
∴EH∥BC，EF∥AD
∴△AEH∽△ABC，△BFE∽△BDA
∴
，
，
即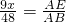
，
，
∴
+
=
+
=
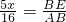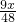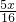=1．
解得：x=2，
∴矩形的周长为：2（5x+9x）=56．
答：矩形的周长为 56．
分析：题中有EF：FG=5：9，要求矩形的周长，只要设EF=5x，EH=FG=9x，利用三角形相似的性质：对应边成比例，可求出x，即可求出周长．
点评：本题考查了相似三角形的性质和判定，对于三角形相似类型的题目求边长，周长等，常常要用相似三角形的对应边成比例的性质来解题，这是常识，应记住并应用．
∵矩形EFGH内接于△ABC且AD⊥BC
∴EH∥BC，EF∥AD
∴△AEH∽△ABC，△BFE∽△BDA
∴
，，即
，，∴
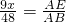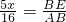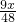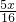+=+==1．解得：x=2，
∴矩形的周长为：2（5x+9x）=56．
答：矩形的周长为 56．
分析：题中有EF：FG=5：9，要求矩形的周长，只要设EF=5x，EH=FG=9x，利用三角形相似的性质：对应边成比例，可求出x，即可求出周长．
点评：本题考查了相似三角形的性质和判定，对于三角形相似类型的题目求边长，周长等，常常要用相似三角形的对应边成比例的性质来解题，这是常识，应记住并应用．
练习册系列答案
考前必练系列答案
相关题目
有一块三角形的材料，需要在其内部裁剪出一块长：宽=4：3的矩形材料，使矩形的一边在三角形底边上，两顶点分别在另外两边上，若设三角形ABC的底边BC=20cm，三角形的高AD=15cm，则该矩形两邻边的长分别为多少厘米？
如图，P是等腰△ABC的底边BC上一点，过点P作BC的垂线，交AB于点Q，交CA的延长线于点R．判断△ARQ是不是等腰三角形，并说明理由．