题目内容
18.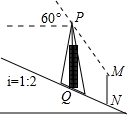 如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2$\sqrt{5}$米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2$\sqrt{5}$米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
分析 如图作MF⊥PQ于F,QE⊥MN于E,则四边形EMFQ是矩形.分别在Rt△EQN、Rt△PFM中解直角三角形即可解决问题.
解答 解:如图作MF⊥PQ于F,QE⊥MN于E,则四边形EMFQ是矩形.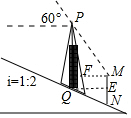
在Rt△QEN中,设EN=x,则EQ=2x,
∵QN2=EN2+QE2,
∴20=5x2,
∵x>0,
∴x=2,
∴EN=2,EQ=MF=4,
∵MN=3,
∴FQ=EM=1,
在Rt△PFM中,PF=FM•tan60°=4$\sqrt{3}$,
∴PQ=PF+FQ=4$\sqrt{3}$+1.
点评 本题考查了解直角三角形的应用-坡度问题,锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.商场计划用于购进这两种商品的费用不超过9000元.
(1)写出y关于x的函数关系式:
(2)该商场至少要购进多少件甲商品?销售完这些商品.商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调m元(50<m<70)出售.且限定商场最多购70件,若商场保持同种商品的售价不变,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
| 商品名称 | 甲 | 乙 |
| 进价(元/件) | 80 | 100 |
| 售价(元/件) | 160 | 240 |
(1)写出y关于x的函数关系式:
(2)该商场至少要购进多少件甲商品?销售完这些商品.商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调m元(50<m<70)出售.且限定商场最多购70件,若商场保持同种商品的售价不变,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
6. 甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
 甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )| 甲 | 乙 | |
| 平均数 | 9 | 8 |
| 方差 | 1 | 1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
3.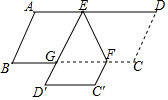 如图,E,F分别是?ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
如图,E,F分别是?ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
 如图,E,F分别是?ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
如图,E,F分别是?ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
10.一个不透明的布袋里装有5个红球,2个白球,3个黄球,它们除颜色外其余都相同,从袋中任意摸出1个球,是黄球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
7.垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
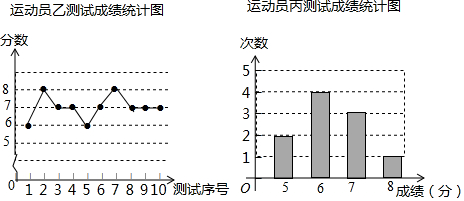
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
运动员甲测试成绩表
| 测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
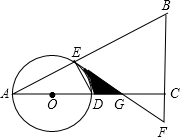 如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.