题目内容
 如图,AB、CD都是BD的垂线,AB=4,CD=6,BD=14.P是BD上一点,连接AP、CP,所得两个三角形相似,则BP的长是
如图,AB、CD都是BD的垂线,AB=4,CD=6,BD=14.P是BD上一点,连接AP、CP,所得两个三角形相似,则BP的长是
- A.2
- B.5.6
- C.12
- D.上述各个值都有可能
D
分析:根据相似三角形对应边比值相等的性质,根据对应边的不同情况即可求得 =
=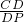 ,
, =
= ,根据AB、CD、BD的长即可求得BP的长,即可解题.
,根据AB、CD、BD的长即可求得BP的长,即可解题.
解答:相似三角形对应边比值相等,分两种情况:
(1) =
=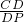 ,则
,则 =
= ,
,
解得BP=5.6,
(2) =
= ,则
,则 =
= ,
,
解得BP=2或12,
故BP=2或12或5.6时,△ABP和△CDP均相似.
故选D.
点评:本题考查了相似三角形对应边比值相等的性质,本题中讨论 =
=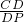 或
或 =
= 是解题的关键.
是解题的关键.
分析:根据相似三角形对应边比值相等的性质,根据对应边的不同情况即可求得
 =
=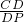 ,
, =
= ,根据AB、CD、BD的长即可求得BP的长,即可解题.
,根据AB、CD、BD的长即可求得BP的长,即可解题.解答:相似三角形对应边比值相等,分两种情况:
(1)
 =
=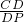 ,则
,则 =
= ,
,解得BP=5.6,
(2)
 =
= ,则
,则 =
= ,
,解得BP=2或12,
故BP=2或12或5.6时,△ABP和△CDP均相似.
故选D.
点评:本题考查了相似三角形对应边比值相等的性质,本题中讨论
 =
=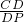 或
或 =
= 是解题的关键.
是解题的关键. 
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
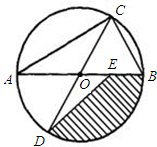 如图,AB和CD都是⊙O的直径,E为OB的中点,若AB=4,AC=
如图,AB和CD都是⊙O的直径,E为OB的中点,若AB=4,AC=
 9、如图,AB和CD都是⊙O的直径,∠AOC=52°,则∠C的度数是( )
9、如图,AB和CD都是⊙O的直径,∠AOC=52°,则∠C的度数是( ) (2012•龙川县二模)如图,AB与CD都是垂直于地面BC的建筑物.在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°,测得顶端D的仰角为36°,若AC=200米,AD=300米,求建筑物CD的高度.(结果保留根号)
(2012•龙川县二模)如图,AB与CD都是垂直于地面BC的建筑物.在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°,测得顶端D的仰角为36°,若AC=200米,AD=300米,求建筑物CD的高度.(结果保留根号) (2012•长春一模)如图,AB、CD都是⊙O的弦,且AB⊥CD.若∠CDB=62°,则∠ACD的大小为( )
(2012•长春一模)如图,AB、CD都是⊙O的弦,且AB⊥CD.若∠CDB=62°,则∠ACD的大小为( ) 如图,AB、CD都是⊙O的弦,且AB∥CD,求证:
如图,AB、CD都是⊙O的弦,且AB∥CD,求证: