题目内容
（2012•长春一模）如图，AB、CD都是⊙O的弦，且AB⊥CD．若∠CDB=62°，则∠ACD的大小为（ ）分析：利用垂直的定义得到∠DPB=90°，再根据三角形内角和定理求出∠B=180°-90°-62°=28°，然后根据圆周角定理即可得到∠ACD的度数．
解答：解：∵AB⊥CD，
∴∠DPB=90°，
∵∠CDB=62°，
∴∠B=180°-90°-62°=28°，
∴∠ACD=∠B=28°．
故选A．
∴∠DPB=90°，
∵∠CDB=62°，
∴∠B=180°-90°-62°=28°，
∴∠ACD=∠B=28°．
故选A．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．
练习册系列答案
相关题目
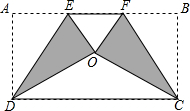（2012•长春一模）将矩形纸片ABCD按如图方式折叠，DE、CF为折痕，折叠后点A和点B都落在点O处．若△EOF是等边三角形，则
（2012•长春一模）如图，抛物线y=ax2-x-
-B于点P，以PQ为一边向右作正方形PQRS，设运动时间为t（秒），正方形PQRS与梯形OABC重叠面积为S（平方单位）