题目内容
【题目】近年来，体育分数在中招考试中占分比重越来越大，不少家长、考生也越来越重视；某中学计划购买一批足球、跳绳供学生们考前日常练习使用，负责此次采购的老师从商场了解到：购买7个足球和4条跳绳共需510元；购买3个足球比购买5条跳绳少50元．
（1）求足球和跳绳的单价；
（2）按学校规划，准备购买足球和跳绳共200件，且足球的数量不少于跳绳的数量的
，请设计出最省钱的购买方案，并说明理由．
【答案】（1）足球的单价为50元/个，跳绳的单价为40元/条；（2）最省钱的购买方案是：购买足球67个，跳绳133条．
【解析】
（1）设足球的单价为x元/个，跳绳的单价为y元/条，根据题意可列出二元一次方程组
，解方程即可得出答案.
（2）设购买足球m个，总费用为w元，则购买跳绳（200﹣m）条，依题意，得：
．由足球的数量不少于跳绳的数量的
，
可得：
，解得：
．再利用一次函数的性质即可解决最值问题.
解：（1）设足球的单价为x元/个，跳绳的单价为y元/条，
依题意，得： ，
解得：
．
答：足球的单价为50元/个，跳绳的单价为40元/条．
（2）设购买足球m个，总费用为w元，则购买跳绳（200﹣m）条，
依题意，得： ．
∵足球的数量不少于跳绳的数量的，
∴ ，
解得： ．
∵m为整数，
∴m≥67．
∵10＞0，
∴w值随m值的增大而增大，
∴当m＝67时，w取得最小值，此时200﹣m＝133．
答：最省钱的购买方案是：购买足球67个，跳绳133条．
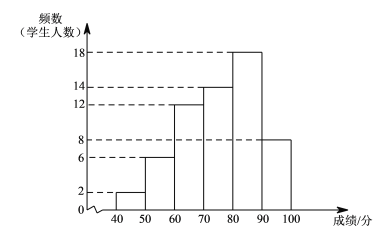
【题目】某年级共有300名学生．为了解该年级学生A，B两门课程的学习情况，从中随机抽取60名学生进行测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和分析．下面给出了部分信息．
．A课程成绩的频数分布直方图如下（数据分成6组：
，
，
，
，
，
）；
．A课程成绩在这一组是：
70 71 71 71 76 76 77 78 
79 79 79 
．A，B两门课程成绩的平均数、中位数、众数如下：
课程 | 平均数 | 中位数 | 众数 |
A |
|
|
|
B |
| 70 | 83 |
根据以上信息，回答下列问题：
（1）写出表中
的值；
（2）在此次测试中，某学生的A课程成绩为76分，B课程成绩为71分，这名学生成绩排名更靠前的课程是________（填“A”或“B”），理由是_______；
（3）假设该年级学生都参加此次测试，估计A课程成绩超过
分的人数．
