Question

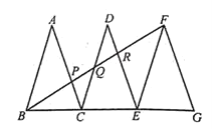
【题目】如图1，点A在x轴上，OA＝4，将OA绕点O逆时针旋转120°至OB的位置．

（1）求经过A、O、B三点的抛物线的函数解析式；

（2）在此抛物线的对称轴上是否存在点P使得以P、O、B三点为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由；

（3 ）如图2，OC＝4，⊙A的半径为2，点M是⊙A上的一个动点，求MC+OM的最小值．

Answer 1

【答案】（1）y＝x2﹣x；（2）存在△POB为等腰三角形，符合条件的点P只有一个，坐标为（2，2）；（3）MC+OM的最小值为CK＝5．

【解析】

（1）设出抛物线解析式，利用待定系数法求出拋物线解析式即可

(2)设点P的坐标为(2，y)，分三种情况讨论，①OB=OP，②2OB=PB，③OP=PB，分别求出y的值，即可得出点P的坐

（3）在OA上取点K，使AK＝1，连接CK交圆与点M，连接OM、CM ，利用△AKM∽△AMO ，求出MC+OM＝MC+KM＝CK，即可解答

（1）如图1，过点B作BD⊥x轴于点D，

∴∠BDO＝90°，

∵OA绕点O逆时针旋转120°至OB，

∴OB＝OA＝4，∠AOB＝120°，B在第二象限，

∴∠BOD＝60°，

∴sin∠BOD＝ ，cos∠BOD＝ ，

∴BD＝ OB＝2 ，OD＝ OB＝2，

∴B（﹣2，2），

设过点A（4，0），B（﹣2，2），O（0，0）的抛物线解析式为y＝ax2+bx+c，

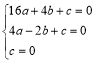∴ 解得： ，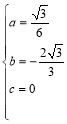

∴抛物线的函数解析式为y＝ x2﹣ x；

（2）存在△POB为等腰三角形，

∵抛物线与x轴交点为A（4，0），O（0，0），

∴对称轴为直线x＝2，

设点P坐标为（2，p），

则OP2＝22+p2＝4+p2，BP2＝（2+2）2+（p﹣2 ）2＝p2﹣4p+28，

①若OP＝OB＝4，则4+p2＝42

解得：p1＝2，p2＝﹣2，

当p＝﹣2时，∠POA＝60°，即点P、O、B在同一直线上，

∴p≠﹣2，

∴P（2，2），

②若BP＝OB＝4，则p2﹣4p+28＝42

解得：p1＝p2＝2，

∴P（2，2）；

③若OP＝BP，则4+p2＝p2﹣4p+28，

解得：p＝2，

∴P（2，2）；

综上所述，符合条件的点P只有一个，坐标为（2，2）；

（3）在OA上取点K，使AK＝1，连接CK交圆与点M，连接OM、CM，

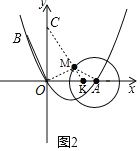
此时，MC+ OM＝MC+KM＝CK为最小值，

理由：∵AK＝1，MA＝2，OA＝4，

∴AM2＝AKOA，而∠MAO＝∠OAM，

∴△AKM∽△AMO，∴ ＝，

即：MC+OM＝MC+KM＝CK，

CK＝ ＝5，

即：MC+OM的最小值为CK＝5．