题目内容
【题目】在![]() 中,若
中,若![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() 分别在
分别在![]() 和
和![]() 上,且
上,且![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() (如图
(如图![]() ),则可以得到以下两个结论:
),则可以得到以下两个结论:
①![]() ;②
;②![]() .
.
那么在![]() 中,仍然有条件“
中,仍然有条件“![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() ,分别在
,分别在![]() 和
和![]() 上”,请探究以下两个问题:
上”,请探究以下两个问题:
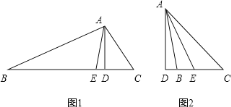
![]() 若
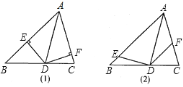
若![]() (如图
(如图![]() ),则
),则![]() 与
与![]() 是否仍相等?若仍相等,请证明;否则请举出反例.
是否仍相等?若仍相等,请证明;否则请举出反例.
![]() 若
若![]() ,则
,则![]() 是否成立?(只写出结论,不证明)
是否成立?(只写出结论,不证明)
【答案】(1)![]() 理由见解析,(2)不一定成立,理由见解析
理由见解析,(2)不一定成立,理由见解析
【解析】
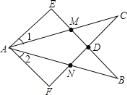
(1)过点D作DM⊥AB于M,DN⊥AC于N,根据角平分线上的点到角的两边的距离相等可得DM=DN,再根据∠AED+∠AFD=180°,平角的定义得∠AFD+∠DFN=180°,可以推出∠DFN=∠AED,然后利用角角边定理证明△DME与△DNF全等,根据全等三角形对应边相等即可证明;
(2)不一定成立,若DE、DF在点D到角的两边的垂线段上或垂线段与点A的两侧,则成立,若是同侧则不成立.
![]() .
.
理由如下:
过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
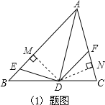
![]() 不一定成立.
不一定成立.
如图,若![]() 、
、![]() 在点
在点![]() 到角的两边的垂线段与顶点
到角的两边的垂线段与顶点![]() 的同侧则一定不成立,
的同侧则一定不成立,
经过![]() 的证明,若在垂线段上或两侧则成立,
的证明,若在垂线段上或两侧则成立,
所以不一定成立.

练习册系列答案
相关题目