题目内容
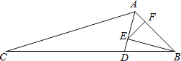
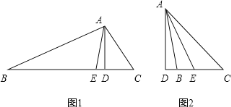
【题目】如图
，在
中，
为
边上的高，
为
的平分线，已知
，
求
的度数；
你发现与
、
之间有何关系？
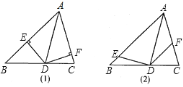
若将“题中的条件”改为“
”如图
，其它条件不变，则与、之间又有何关系？请说明理由．
若将“题目中的条件，”改为“
，
”，其它条件不变，求、的度数．
【答案】（1）
；（2）
；（3）
（4）
，
．
【解析】
（1）首先根据三角形内角和定理求得∠BAC，再根据角平分线的定义求得∠BAE，再根据三角形的一个外角等于和它不相邻的两个内角和求得∠AED，最后根据直角三角形的两个锐角互余即可求解；（2）根据（1）即可得出∠EAD与∠B、∠C之间的关系；（3）根据三角形内角和定理、角平分线的性质、三角形外角的性质依次推理即可得出结论；（4）根据（3）中结论及三角形内角和定理即可得出答案.
解：
∵
，
，
∴
．
又
是
的角平分线，
∴
，
∴
，
又
是
边上的高，
∴，
由图知，
，
由图知：
，
根据得：
，
根据三角形内角和定理得：
，
解得：，．
练习册系列答案
相关题目
【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克，其中各种糖果的单价和千克数如表所示，商家用加权平均数来确定什锦糖的单价．
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价（元/千克） | 15 | 25 | 30 |
千克数 | 40 | 40 | 20 |
（1）求该什锦糖的单价．
（2）为了使什锦糖的单价每千克至少降低2元，商家计划在什锦糖中加入甲、丙两种糖果共100千克，问其中最多可加入丙种糖果多少千克？
