题目内容
1.已知等腰△ABC,AB=AC,现将△ABC折叠,使点A,B两点重合,折痕所在的直线与直线AC的夹角为40°,则∠B的度数为65°或25°.分析 首先根据题意画出图形,如图1,如图1:由翻折的性质可知:EF⊥AB,所以∠A+∠AFE=90°,从而可求得∠A=50°,然后根据等腰三角形的性质和三角形的内角和定理可求得∠B=65°;如图2;由翻折的性质可知:EF⊥AB,∠D+∠DAE=90°,故此∠DAE=50°,然后由等腰三角形的性质和三角形的外角的性质可求得∠B=25°.
解答 解:如图1:
由翻折的性质可知:EF⊥AB,
∴∠A+∠AFE=90°.
∴∠A=90°-40°=50°,
∵AB=AC,
∴∠B=∠C.
∴∠B=$\frac{1}{2}$×(180°-∠A)=$\frac{1}{2}×(180°-50°)$=65°;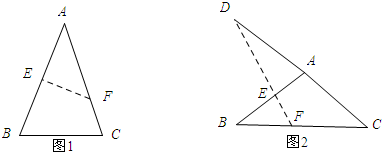
如图2;由翻折的性质可知:EF⊥AB,
∴∠D+∠DAE=90°.
∴∠DAE=90°-40°=50°,
∵AB=AC,
∴∠B=∠C.
∵∠B+∠C=∠DAE,
∴∠B=$\frac{1}{2}$∠DAE=$\frac{1}{2}×50°$=25°.
点评 本题主要考查的是翻折的性质和等腰三角形的性质,根据题意画出符合题意的图形是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
12.下列命题的逆命题正确的是( )
| A. | 如果两个角是直角,那么它们相等 | B. | 全等三角形的面积相等 | ||
| C. | 同位角相等,两直线平行 | D. | 若a=b,则a2=b2 |

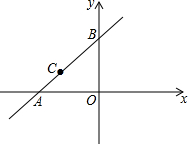 如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.
如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.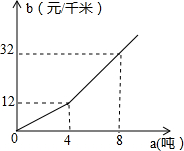 某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.