Question

【题目】综合与探究：

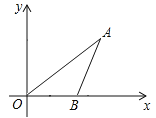
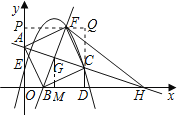
如图1，的直角顶点在坐标原点，点在轴正半轴上，点在轴正半轴上，，，将线段绕点顺时针旋转得到线段，过点作轴于点，抛物线经过点，与轴交于点，直线与轴交于点．

（1）求点的坐标及抛物线的表达式；

（2）如图2，已知点是线段上的一个动点，过点作的垂线交抛物线于点（点在第一象限），设点的横坐标为．

①点的纵坐标用含的代数式表示为________；

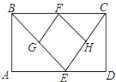
②如图3，当直线经过点时，求点的坐标，判断四边形的形状并证明结论；

③在②的前提下，连接，点是坐标平面内的点，若以，，为顶点的三角形与全等，请直接写出点的坐标．

Answer 1

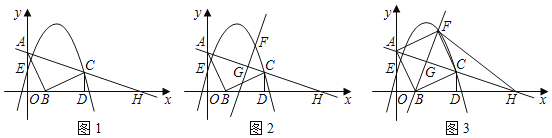
【答案】（1）点的坐标为，；（2）①；②点F的坐标为，四边形为正方形，证明见解析；③点的坐标为或或．

【解析】

（1）根据已知条件与旋转的性质证明，根据全等三角形的性质得出点C的坐标，结合点E的坐标，根据待定系数法求出抛物线的表达式；

（2）①设直线AC的表达式为，由点A、C的坐标求出直线AC的表达式，进而得解；

②过点作轴于点，过点作轴，垂足为点，的延长线与的延长线交于点，根据等腰三角形三线合一得出，结合①由平行线分线段成比例得出点G的坐标，根据待定系数法求出直线的表达式，结合抛物线的表达式求出点F；利用勾股定理求出，结合可得出结论；

③根据直线AC的表达式求出点H的坐标，设点N坐标为，根据勾股定理分别求出，，，，然后分两种情况考虑：若△FHC≌△FHN，则FN＝FC，NH＝CH，若△FHC≌△HFN，则FN＝CH，NH＝FC，分别列式求解即可．

解：（1），，

点的坐标为，点的坐标为，

线段绕点顺时针旋转得到线段，

，，

，

在中，，

，

轴于点，

，

．

，

，

，，

，

点的坐标为，

∵抛物线的图象经过点，与轴交于点，

，

解得，，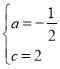

∴抛物线的表达式为；

（2）①设直线AC的表达式为，

∵直线AC经过点，，

∴，

解得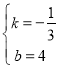，，即，

∴点的纵坐标用含的代数式表示为：，

故答案为：．

②过点作轴于点，

，，

，，

，

，

，

，

，

，，

点为，

设直线的表达式为，将和代入表达式得，，

，即表达式为，

点为直线和抛物线的交点，

得，

，（舍去），

点的坐标为，

过点作轴，垂足为点，的延长线与的延长线交于点，

，，，，

在中和中，根据勾股定理，得，

同理可得，

，

四边形为菱形，

，

菱形为正方形；

③∵直线AC：与x轴交于点H，

∴，

解得，x＝12，

∴，

∴，，

设点N坐标为，

∴，，

第一种情况：若△FHC≌△FHN，则FN＝FC，NH＝CH，

∴，

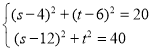解得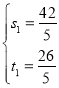，，（即点C），

∴；

第二种情况：若△FHC≌△HFN，则FN＝CH，NH＝FC，

∴，

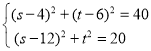解得，，，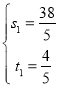

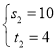∴或，

综上所述，以F，H，N为顶点的三角形与△FHC全等时，点N坐标为或或．