题目内容
 如图,在△ABC中,∠C=90°,点G是△ABC的重心,且AG⊥CG.
如图,在△ABC中,∠C=90°,点G是△ABC的重心,且AG⊥CG.(1)求证:△CAG∽△ABC;
(2)求sinB的值.
考点:三角形的重心,相似三角形的判定与性质
专题:计算题
分析:(1)证明:CG交AB于D,如图,设GD=a,根据重心的性质得CG=2DG=2a,根据重心的定义得CD为AB边上的中线,接着根据直角三角形斜边上的中线性质得到CD=AD=BD=3a,则∠1=∠3,再利用等角的余角相等得∠1=∠3,所以∠B=∠3,加上∠ACB=∠AGC=90°,于是根据相似三角形的判定方法得到△CAG∽△ABC;
(2)根据相似的性质,由△CAG∽△ABC得到
=
,则可计算出AC=2
a,然后在Rt△ACB中,利用正弦的定义求解.
(2)根据相似的性质,由△CAG∽△ABC得到
| AC |
| AB |
| CG |
| AC |
| 3 |
解答:(1)证明:CG交AB于D,如图,设GD=a,
∵点G是△ABC的重心,
∴CG=2DG=2a,CD为AB边上的中线,
∴CD=AD=BD=3a,
∴∠1=∠3,
∵AG⊥CG,
∴∠2+∠3=90°,
而∠1+∠2=90°,
∴∠1=∠3,
∴∠B=∠3,
而∠ACB=∠AGC=90°,
∴△CAG∽△ABC;
(2)解:∵△CAG∽△ABC,
∴
=
,即
=
,
∴AC=2
a,
在Rt△ACB中,sinB=
=
=
.

∵点G是△ABC的重心,
∴CG=2DG=2a,CD为AB边上的中线,
∴CD=AD=BD=3a,
∴∠1=∠3,
∵AG⊥CG,
∴∠2+∠3=90°,
而∠1+∠2=90°,
∴∠1=∠3,
∴∠B=∠3,
而∠ACB=∠AGC=90°,
∴△CAG∽△ABC;
(2)解:∵△CAG∽△ABC,
∴
| AC |
| AB |
| CG |
| AC |
| AC |
| 6a |
| 2a |
| AC |
∴AC=2
| 3 |
在Rt△ACB中,sinB=
| AC |
| AB |
2
| ||
| 6a |
| ||
| 3 |
点评:本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查相似三角形的判定与性质.

练习册系列答案
相关题目
下列式子正确的是( )
| A、a3•a3=2a3 | ||||
| B、a6÷a2=a3 | ||||
C、(
| ||||
| D、(a-b)2=a2-b2 |
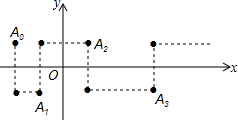 如图,将点A0(-2,1)作如下变换:作A0关于x轴对称点,再往右平移1个单位得到点A1,作A1关于x轴对称点,再往右平移2个单位得到点A2,…,作An-1关于x轴对称点,再往右平移n个单位得到点An(n为正整数),则点A63的坐标为( )
如图,将点A0(-2,1)作如下变换:作A0关于x轴对称点,再往右平移1个单位得到点A1,作A1关于x轴对称点,再往右平移2个单位得到点A2,…,作An-1关于x轴对称点,再往右平移n个单位得到点An(n为正整数),则点A63的坐标为( )| A、(2016,-1) |
| B、(2015,-1) |
| C、(2014,-1) |
| D、(2013,-1) |
 如图,直线m表示一条公路,公路两旁有两个村庄A、B,现要在公路上修建一个车站,使车站到两村的路程之和最短,请在直线m上作出车站P的位置,你这样确定的理由是
如图,直线m表示一条公路,公路两旁有两个村庄A、B,现要在公路上修建一个车站,使车站到两村的路程之和最短,请在直线m上作出车站P的位置,你这样确定的理由是 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,则当x=9时,等腰△AEF的面积为
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,则当x=9时,等腰△AEF的面积为 如图所示,一个水平放置的长方形水槽长18dm,宽12dm,高9dm,水深4dm,一个棱长为6dm的立方体铁块,以底面平行于液面的方式逐步没入水中,设铁块没入水中的高度为xdm,同时水面上升的相应高度为ydm,写出y关于x的函数表达式
如图所示,一个水平放置的长方形水槽长18dm,宽12dm,高9dm,水深4dm,一个棱长为6dm的立方体铁块,以底面平行于液面的方式逐步没入水中,设铁块没入水中的高度为xdm,同时水面上升的相应高度为ydm,写出y关于x的函数表达式