Question

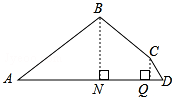
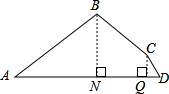有一块四边形的地ABCD（如图所示），测得AB=26m，BC=10m，CD=5m，顶点B，C到AD的距离分别为10m，4m，则这块地的面积为

 

m²．

Answer 1

分析：如图把图形分解成△ABN和△CDQ、梯形BNQC求解．

解答：解：∵S_{四边形ABCD}=S_△ABN+S_梯形BCQN+S_△CDQ=

1

2

AN•BN+

1

2

（BN+CQ）•NQ+

1

2

QD•CQ
且BN=10，CQ=4，AB=26，BC=10，CD=5，
AN=

AB2-BN2

=

262-102

=24，
NQ=

BC2-(BN-CQ)2

=

102-62

=8，
QD=

CD2-CQ2

=

52-42

=3，
∴S_{四边形ABCD}=

1

2

×24×10+

1

2

×（10+4）×8+

1

2

×3×4=182（m²）．
故答案为：182．

点评：本题利用了勾股定理，三角形和梯形的面积公式求解，求解不规则图形的面积，常常作辅助线，把它分成三角形和特殊的四边形求解．