题目内容
如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=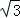 ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.
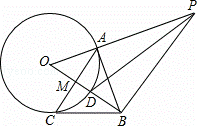
(1)证明:连结OC,如图,
∵AC⊥OB,
∴AM=CM,
∴OB为线段AC的垂直平分线,
∴BA=BC,
在△OAB和△OCB中
 ,
,
∴△OAB≌△OCB,
∴∠OAB=∠OCB,
∵OA⊥AB,
∴∠OAB=90°,
∴∠OCB=90°,
∴OC⊥BC,
∴BC是⊙O的切线;
(2)解:在Rt△OAB中,OA=1 ,AB=
,AB=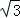 ,
,
∴OB= =2,
=2,
∴∠ABO=30°,∠AOB=60°,
∵PB⊥OB,
∴∠PBO=90°,
在Rt△PBO中,OB=2,∠BPO=30°,
∴PB= OB=2
OB=2 ,
,
在Rt△PBD中,BD=OB﹣OD=2﹣1=1,PB=2 ,
,
∴PD= =
= ,
,
∴sin∠BPD= =
= =
= .
.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某工程队准备修建一条长1200m的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前2天完成任务.若设原计划每天修建道路xm,则根据题意可列方程为( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
如图所示的立体图形,它的正视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
﹣ 的相反数是( )
的相反数是( )
|
| A. |
| B. | ﹣ | C. | 7 | D. | ﹣7 |
 ﹣
﹣ =2
=2 ﹣
﹣ ﹣
﹣ =2
=2 =2
=2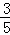 ,求⊙O的直径.
,求⊙O的直径.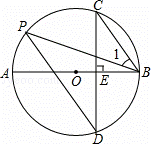
 )÷
)÷ ,其中x=3.
,其中x=3.



 有意义时,x的取值范围为
有意义时,x的取值范围为  .
.