题目内容
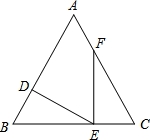
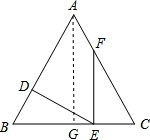
在△ABC中,AB=AC=5,BC=6,点D在边AB上,DE⊥AB,点E在边BC,点F在边AC上,且∠DEF=∠B.
(1)求证:△FCE∽△EBD;
(2)当点D在线段AB上运动时,是否有可能使S△FCE=4S△EBD?如果有可能,那么求出BD的长;如果不可能,请说明理由.
【考点】相似三角形的判定与性质.
【分析】(1)由AB=AC,DE⊥AB,得到∠B=∠C,∠BDE=90°,由∠B=∠DEF,证得∠BDE=∠FEC=90°,于是可证得结论.
(2)作AG⊥BC,根据等腰三角形的性质得到BG=3,根据△FCE∽△EBD,得到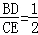 ,由△BDE∽△BGA,得到
,由△BDE∽△BGA,得到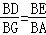 ,设BD=x,CE=2x,求得BD=
,设BD=x,CE=2x,求得BD=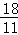 ,
,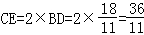 ,根据△ECF∽△GCA,由相似三角形的性质得到
,根据△ECF∽△GCA,由相似三角形的性质得到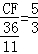
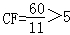 ,即可得到结论.
,即可得到结论.
【解答】证明:(1)∵AB=AC=5,DE⊥AB,
∴∠B=∠C,∠BDE=90°,
∵∠B=∠DEF,
∴∠B+∠BDE=∠DEF+∠FEC,
∴∠BDE=∠FEC=90°,
∵在△FCE和△EBD中,
∠B=∠C,∠BDE=∠FEC,
∴△FCE∽△EBD;
(2)作AG⊥BC,
∵AB=AC=5,BC=6,AG⊥BC,
∴BG=3,
∵S△FCE=4S△EBD,
∴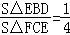 ,
,
∵△FCE∽△EBD,
∴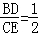 ,
,
∵在△BDE和△BGA中,
∠B=∠B,∠BDE=∠BGA,
∴△BDE∽△BGA,
∴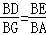 ,
,
设BD=x,CE=2x,
∴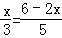 ,
,
解得:x=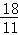 ,
,
∴BD=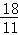 ,
, ,
,
∵△ECF∽△GCA,
∴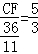
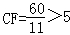 ,
,
∴不可能在线段AB上存在D点,使S△FCE=4S△EBD.
【点评】本题考查的是相似三角形的判定与性质,等腰三角形的性质,三角形面积的计算,根据题意画出图形利用数形结合是解答此题的关键.

练习册系列答案
相关题目
 .
.
 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,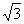 ).
).

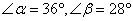 ,则
,则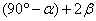 =
= 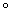 .
.